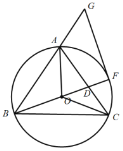
题目内容
【题目】如图，在矩形
中，
，
，点
在线段
上，由点
向点
运动，当点与点重合时，停止运动．以点为圆心，
为半径作
，与交于点
，点
在上且在矩形外，
．
（1）当
时，
__________，扇形
的面积=__________，点
到的最短距离=__________．
（2）与
相切时，求
的长？
（3）如图与交于点
、
，当
时，求的长？
（4）请从下面两问中，任选一道进行作答．
①当与
有两个公共点时，直接写出的取值范围．
②直接写出点的运动路径长以及
的最短距离．
【答案】（1）
，
，
；（2）
；（3）4；（4）①
，或
；②
，
【解析】
（1）根据已知直接可求；
（2）⊙P与AC相切时，设切点为点H，连接PH，则PH⊥AC，在Rt△ADC中，AB=6，BC=8，得AC=10；在Rt△ADC中，sin∠DAC=
，设⊙P半径为x，则PH=PD=x，AP=8-x，在Rt△AHP中，sin∠PAH=
＝
，可求x=3，在Rt△PDC中，CD=6，PD=3，求得PC=
；
（3）过点P作PH⊥AC，连接PF；则∠PHA=∠ADC=90°，可证△AHP∽△ADC，设⊙P半径为x，则PF=PD=x，AP=8-x，则PH=（8-x），在⊙P中，FH⊥AC，EF=6.4，HF=3.2，在Rt△PHF中，((8x))2+3.22=x2，求得PD=4；
（4）①作PM⊥AC于M，作PN⊥BC于N，易知PM=PD时，⊙P与AC相切，与△ABC只有一个公共点，PM＜PD时⊙P与△ABC没有公共点；当PN=PD时，⊙P与BC相切，⊙P与△ABC有三个公共点，当PB=PD时，⊙P与△ABC有三个公共点；当PB＜PD≤AD时，⊙P与△ABC有且只有两个公共点；故3＜PD＜6或
＜PD≤8；②由∠QPD=120°，PQ=PD可得：∠ADQ=30°，即Q的路径是一条线段，且线段DQ位于AD上方，易求得DQ=8
，BQ的最短距离即点B到DQ的垂线段长度，可求得span>DQ的最小值=3+4；
解：（1）如图1，连接PC，QP，PC交⊙P于T，
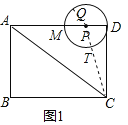
∵矩形ABCD
∴∠ADC=90°，CD=AB=6，AD=BC=8，
在Rt△CDP中，由勾股定理得：PC=
=
=4 ，
∵∠QPD=120°，PD=2
∴S扇形QPD＝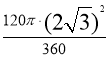
=4π
CT=CP-PT=4-2=2
故答案为：4，4π，2；
（2）
与
相切时，设切点为点
，
连接
，则
，
四边形
为矩形
在
中，
，
，
在中，
设半径为
，则
，
，
在
中，
，
，
在
中，
，
，
（3）过点
作，垂足为点，连接
，
则
又
设半径为，则
，，
在中，，
在
中，根据勾股定理得：
解得：
（舍去），
的长为4．
（4）①，或
②，
