题目内容
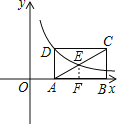
【题目】如图,矩形ABCD中,E是AC的中点,点A、B在x轴上.若函数![]() (
(![]() )的图像过D、E两点,则矩形ABCD的面积为______.
)的图像过D、E两点,则矩形ABCD的面积为______.

【答案】16
【解析】分析:过E作EF⊥AB于F,由三角形中位线定理可得AD=2EF,设点D的横坐标为m,D点坐标为(m,![]() ),得出AD=
),得出AD=![]() ,即可得出EF=
,即可得出EF=![]() ,根据图象上的坐标特征得出E的横坐标为2m,继而得出AB=2m,然后根据矩形的面积公式即可求得.
,根据图象上的坐标特征得出E的横坐标为2m,继而得出AB=2m,然后根据矩形的面积公式即可求得.
详解:过E作EF⊥AB于F,
∵点E是矩形ABCD对角线的交点,
∴AE=CE,
∴EF是△ABC的中位线,
∴AD=2EF,
设点D的横坐标为m,且点D在反比例函数y=![]() (x>0)上,
(x>0)上,
∴D点坐标为(m,![]() ),
),
∴AD=![]() ,
,
∴EF=![]() ,
,
∴E(2m,![]() ),
),
∴AF=m,
∴AB=2m,
∴矩形ABCD的面积=2m![]() =16,
=16,
故答案为16.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目