Question

【题目】如图，A，B两点在反比例函数y＝的图象上，C，D两点在反比例函数y＝的图象上，AC⊥x轴于点E，BD⊥x轴于点F，AC＝2，BD＝3，EF＝，则k2－k1的值为( )

A. 4 B. C. D. 6

Answer 1

【答案】A

【解析】连接OA、OC、OD、OB，如图：

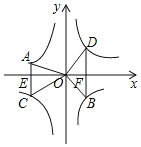
由反比例函数的性质可知S△AOE=S△BOF=|k1|=-k1，S△COE=S△DOF=k2，

∵S△AOC=S△AOE+S△COE，

∴ACOE=×2OE=OE=（k2-k1）…①，

∵S△BOD=S△DOF+S△BOF，

∴BDOF=×3（EF-OE）=×3（-OE）=5-OE=（k2-k1）…②，由①②两式解得OE=2，

则k2-k1=4．

点睛:一般的，从反比例函数图像上任一点P，向x轴和y轴作垂线你，以点P的两个垂足及坐标原点为顶点的矩形面积等于常数