题目内容
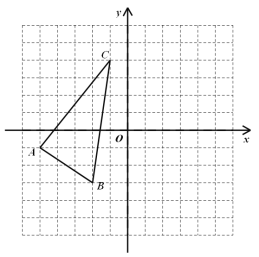
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点.
两点.
(1)求线段AB的长度;
(2)若点![]() 在第二象限,且△
在第二象限,且△![]() 为等腰直角三角形,求点
为等腰直角三角形,求点![]() 的坐标;
的坐标;

【答案】(1)5(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)
【解析】
(1)先求出A,B的坐标,根据勾股定理,得到AB的长;
(2)分三种情况分别进行讨论.
解:(1)当x=0,得y=3,
当y=0,x=-4,
∴A(-4,0),B(0,3),即OA=4,OB=3,
∴根据勾股定理AB=5;
(2)①过点A作C1A⊥AB,截取AC1=AB,此时△AC1B是等腰直角三角形,
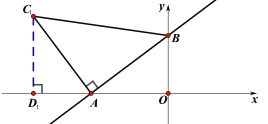
过C1作C1D1⊥x轴于D1,此时Rt△C1D1A≌Rt△AOB,
∴C1D1=OA=4,AD1=OB=3,OD1=7,
∴C1(-7,4);
②过点B作C2B⊥AB,截取BC2=AB,此时△AC2B是等腰直角三角形,
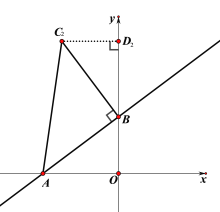
过C2作C2D2⊥y轴于D2,此时Rt△C2D2B≌Rt△BOA,
∴C2D2=OB=3,BD2=OA=4,OD2=7,
∴C2(-3,7);
③以AB为腰,作等腰直角△AC3B,
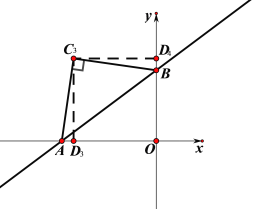
过C3作C3D3⊥OA,作C3D4⊥OB,此时Rt△C3D3A≌Rt△C3D4B,四边形C3D3OD4是正方形,
∴AD3=BD4,
∴OA-AD3=OB+BD4,即4-AD3=3+BD4,
∴AD3=BD4=![]() ,
,
∴OD3=4-![]() ,OD4=3+
,OD4=3+![]() =
=![]() ,
,
∴C3(-![]() ,
,![]() ).
).
故答案为:(1)5;(2)(-3,7)(-7,4)(-![]() ,
,![]() )
)

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目