题目内容
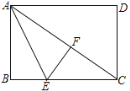
【题目】如图,已知ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)若M为AG中点,且DM=2,求DE的长;
(2)求证:AB=CF+DM.

【答案】(1)DE=![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由ABCD中,AE平分∠BAD交DC于E,DF⊥BC,易证得∠DMG=∠DGM,求得DG=DM=2,由直角三角形斜边上的中线等于斜边上的一半,求得AG的长,继而求得DE的长;
(2)此题有多种解法,通过构造不同的直角三角形,找到相应的全等三角形,在根据对应边和对应角相等,即可推出结论.
解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠BAE=∠DEA,
∵AE平分∠BAD,∴∠BAE=∠DAE
∴∠DAE=∠DEA,
∴DE=AD,
∵DF⊥BC,
∴DF⊥AD,
∵M为AG中点,
∴AG=2DM=4,
∵DN⊥CD,
∴∠ADM+∠MDG=∠MDG+∠EDG,
∴∠ADM=∠EDG,
∴∠DAE+∠ADM=∠DEA+∠EDG,
即∠DMG=∠DGM,
∴DG=DM=2,
在Rt△ADG中,DE=AD=![]() =
=![]() ;
;
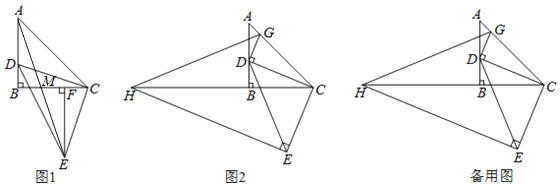
(2)证法一:过点A作AD的垂线交DN的延长线于点H,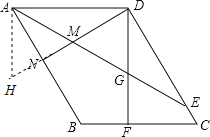
在△ADH和△FDC中,
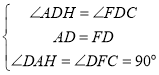 ,
,
∴△DAH≌△DFC(ASA),
∴AH=FC,DH=DC,
∵DF⊥AD,
∴AH∥DF,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,∠DMG=∠DGM,
∴∠HAM=∠HMA,
∴AH=MH,
∴MH=CF,
∴AB=CD=DH=MH+DM=CF+DM.
证法二:延长MD到点P,使DP=CF,连接PE
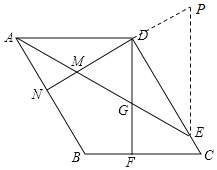
由(1)知AD=DE,
又AD=DF,
∴DF=DE,
∠DFC=∠EDP=90°
∴Rt△DCF≌Rt△EPD,
∴DC=EP,∠CDF=∠PED
∴PE∥DF,
∴∠PEA=∠DGA,
由(1)得∠DGA=∠DME,
∴∠PEA=∠DME
∴PM=PE,
而PM=DM+DP=DM+CF,PE=CD=AB,
∴AB=DM+FC.
证法三:过点A作AH⊥CB于点H,
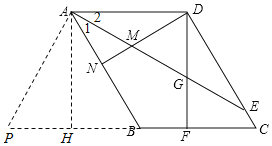
易证△ABH≌△DCF,
从而证得四边形AHFD为正方形.
把△ADG绕点A顺时针旋转90°,
得△AHP,∠AHP=∠AHB=90°
∴P、H、B三点共线
∵AE平分∠BAD,
∴∠1=∠2,而∠2=∠HAP,
∴∠HAB+∠1=∠HAB+∠HAP,即∠HAG=∠PAB
∵AH∥DF,
∴∠HAG=∠DGA
而∠DGA=∠APB
∴∠PAB=∠APB
∴AB=PB
∵PB=PH+HB=DG+FC
∴AB=DM+FC.
证法四:在DC上截取DP=DM,连接PF,

∵四边形ABCD是平行四边形,
∴AB∥CD
∴∠BAE=∠DEA,
而∠BAE=∠DAE,
∴∠DAE=∠DEADA=DE,
又∠ADF=∠MDE=90°,
∴∠ADM=∠EDG,
∴△ADM≌△EDG,
∴DM=DG,
∴DG=DP,
又AD=DF,
∴DF=DE,而∠PDF=∠FDP,
∴△PDF≌△GDE,
∴∠DPF=∠DGE,∠DFP=∠DEG,
∴∠CPF=∠DGM,
∵∠DFP+∠CFP=∠DEG+∠DMG=90°,
∴∠CFP=∠DMG,
而∠DMG=∠DGM,
∴∠CFP=∠CPFCF=CP,
而CD=DP+CP=DM+CF,AB=CD,
∴AB=DM+CF.