题目内容
【题目】已知关于 x 的一元二次方程 x![]() ﹣(m+2)x+3m﹣3=0.
﹣(m+2)x+3m﹣3=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于-2,求 m 的取值范围.
【答案】(1)见解析;(2)m 的取值范围为 m<-1.
【解析】
(1)根据方程的系数结合根的判别式,可得![]() ,由此可证出方程总有两个实数根;
,由此可证出方程总有两个实数根;
(2)利用公式法解一元二次方程,可得出x=3 或 x=m-1,根据方程有一根小于-2,即可得出关于m的一元一次不等式,解之即可得出m的取值范围.
(1)证明:∵关于 x 的一元二次方程 ![]() -(m+2)x+3m=0,
-(m+2)x+3m=0,
∴![]() ,
,
∴方程总有两个实数根;
(2)由求根公式得: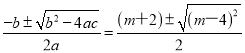
解得:x=3 或x=m-1,
若方程有一个根小于-2,则 ![]() ,
,
解得:![]() .
.
答:若方程有一个根小于-2,m 的取值范围为![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目