题目内容
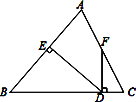
【题目】如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.
(1)求证:DF是线段AB的垂直平分线;
(2)当AB=AC,∠A=46°时,求∠EBC及∠F的度数.

【答案】(1)见解析;(2)∠EBC =21°,∠F=23°.
【解析】试题分析:(1)、根据题意得出AE=BE,然后结合AD=BD得出答案;(2)、根据等腰三角形的性质得出∠ABC=∠ACB=67°,根据∠EBC=∠ABC﹣∠ABE和∠F=90°﹣∠ABC得出角度.
试题解析:(1)、证明:∵∠A=∠ABE, ∴EA=EB, ∵AD=DB,
∴DF是线段AB的垂直平分线;
(2)、解:∵∠A=46°, ∴∠ABE=∠A=46°, ∵AB=AC, ∴∠ABC=∠ACB=67°,
∴∠EBC=∠ABC﹣∠ABE=21°, ∠F=90°﹣∠ABC=23°.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目