��Ŀ����
����Ŀ����ͼ����֪��![]() �У�
�У�![]() Ϊ
Ϊ![]() ���е㣮
���е㣮
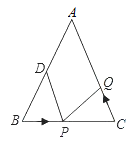
��1�������![]() ���߶�
���߶�![]() ����
����![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶���ͬʱ����
�˶���ͬʱ����![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ���
���![]() �˶���
�˶���
������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶ���ȣ�
���˶��ٶ���ȣ�![]() ��
��![]() ��
��![]() �Ƿ�ȫ�ȣ���˵������
�Ƿ�ȫ�ȣ���˵������
������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶȲ���ȣ����
���˶��ٶȲ���ȣ����![]() ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ
���˶��ٶ�Ϊ����ʱ���ܹ�ʹ![]() ��
��![]() ȫ�ȣ�
ȫ�ȣ�
��2������![]() �Ե�
�Ե�![]() ����е��˶��ٶȴӵ�
����е��˶��ٶȴӵ�![]() ��������
��������![]() ��ԭ�����˶��ٶȴӵ�
��ԭ�����˶��ٶȴӵ�![]() ͬʱ����������ʱ����
ͬʱ����������ʱ����![]() �����˶�����������ʱ�䣬��
�����˶�����������ʱ�䣬��![]() ���
���![]() ��һ����
��һ����![]() ����������������
����������������
���𰸡���1����ȫ�ȣ����ɼ���������3.75cm/s����2��![]() s��AB����
s��AB����
��������
��1���������BP=CQ=3��PC=BD=5��Ȼ����ݵȱ߶ԵȽ���á�B=��C���ٸ���SAS����֤����
����BPD����CQP������BP=CP��BD=CQ�����Q���ٶ�Ϊv������t��ֱ�����BP=CP��BD=CQ����������ɵó������
��3���辭��x����P���Q��һ����������������ʱ��·�̲�Ϊ10+10���������ʱ��x��ֵ��ȷ��P���˶�·�̣�����һ�ܵij�������𰸼��ɣ�
��1���١�t=1���룩��
��BP=CQ=3�����ף�
��AB=10��DΪAB�е㣬
��BD=5�����ף�
�֡�PC=BC-BP=8-3=5�����ף�
��PC=BD
��AB=AC��
���B=��C��
����BPD����CQP��
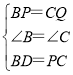 ��
��
���BPD�ա�CQP��SAS����
�����Q���ٶ�Ϊv������t����BPD��ա�CQP��
Ҫʹ��BPD�ա�CQP����������BD��CQ��BP��PC��
��![]() ��
��
���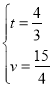 ��
��
�𣺵�Q���˶��ٶ�Ϊ![]() ����/��ʱ���ܹ�ʹ��BPD�ա�CQP��
����/��ʱ���ܹ�ʹ��BPD�ա�CQP��
��2���辭��x����P���Q��һ���������������
![]() x��3x+2��10��
x��3x+2��10��
���x��![]() ��
��
��P���˶���![]() ��3��80���ף�
��3��80���ף�
80����8+10+10����2![]() 24�����˶���2Ȧ�����˶���24���ף����ʱ�˶���AB�ϣ�
24�����˶���2Ȧ�����˶���24���ף����ʱ�˶���AB�ϣ�
�𣺾���![]() �룬��P��Q�ڵ�һ���ڱ�AB��������
�룬��P��Q�ڵ�һ���ڱ�AB��������

 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�