题目内容
【题目】如图,ABCD的顶点A,B的坐标分别是A(﹣1,0),B(0,﹣3),顶点C,D在双曲线y= ![]() 上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= .
上,边AD交y轴于点E,且ABCD的面积是△ABE面积的8倍,则k= . 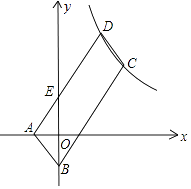
【答案】36
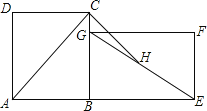
【解析】解:如图,过C、D两点作x轴的垂线,垂足为F、G,DG交BC于M点,过C点作CH⊥DG,垂足为H, ∵ABCD是平行四边形,
∴∠ABC=∠ADC,
∵BO∥DG,
∴∠OBC=∠GDE,
∴∠HDC=∠ABO,
∴△CDH≌△ABO(AAS),
∴CH=AO=1,DH=OB=3,设C(m+1,n),D(m,n+3),
则(m+1)n=m(n+3)=k,
解得n=3m,则D的坐标是(m,3m+3),
设直线AD解析式为y=ax+b,将A、D两点坐标代入得![]() ,
,
由①得:a=b,代入②得:mb+b=3m+3,
即b(m+1)=3(m+1),解得b=3,
则 ![]() ,
,
∴y=3x+3,E(0,3),BE=6,
∴S△ABE= ![]() ×BE×AO=3,
×BE×AO=3,
∵S四边形ABCD=8S△ABE=24,
∴S四边形ABCD=2S△ABE+S四边形BEDM=24,
即6+6×m=24,
解得m=3,
∴n=3m=9,
∴k=(m+1)n=4×9=36.
所以答案是:36.
【考点精析】通过灵活运用比例系数k的几何意义和平行四边形的性质,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目