题目内容
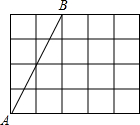 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是
- A.1个
- B.2个
- C.3个
- D.4个
D
分析:利用等腰三角形的定义,并结合勾股定理,找到一点,使其与AB组成的三角形中有两条边相等,就可判断解答.
解答: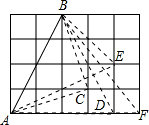 解:如图,在△ABC中,AC=
解:如图,在△ABC中,AC=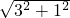 =
= ,
,
BC=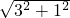 =
= ,即,AC=AB,
,即,AC=AB,
所以,△ABC为等腰三角形;
同理,可取得点D、点E、点F,
在△ABD、△ABE、△ABF中,
AB=BD= =
= ,
,
AB=AE= =
= ,
,
AF=5,BF= =5,
=5,
所以,△ABD、△ABE、△ABF为等腰三角形.
故选D.
点评:本题考查了等腰三角形的判定;利用等腰三角形的判定来解决特殊的问题,其关键是根据题意,画出符合实际条件的图形,再利用数学知识来求解.
分析:利用等腰三角形的定义,并结合勾股定理,找到一点,使其与AB组成的三角形中有两条边相等,就可判断解答.
解答:
 解:如图,在△ABC中,AC=
解:如图,在△ABC中,AC=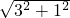 =
= ,
,BC=
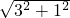 =
= ,即,AC=AB,
,即,AC=AB,所以,△ABC为等腰三角形;
同理,可取得点D、点E、点F,
在△ABD、△ABE、△ABF中,
AB=BD=
 =
= ,
,AB=AE=
 =
= ,
,AF=5,BF=
 =5,
=5,所以,△ABD、△ABE、△ABF为等腰三角形.
故选D.
点评:本题考查了等腰三角形的判定;利用等腰三角形的判定来解决特殊的问题,其关键是根据题意,画出符合实际条件的图形,再利用数学知识来求解.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
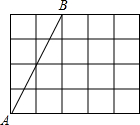 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
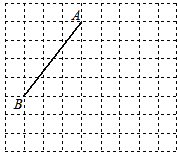 向旋转90°得到线段AC.
向旋转90°得到线段AC. 33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由).
33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由).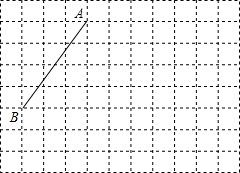 如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC. (2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.
(2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.