题目内容
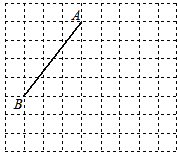
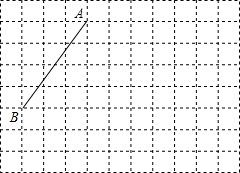 如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.
如图:线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.(1)请你在所给的网格中画出线段AC及点B经过的路径;
(2)若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),则点C的坐标为
(3)线段AB绕点A按逆时针方向旋转90°得到线段AC,若有一张与线段AB扫过的区域形状、大小相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径为
(4)在图中确定格点E,并画出一个以A、B、C、E为顶点的四边形,使其为中心对称图形.
分析:(1)根据旋转图形前后不发生任何变化,找出AB坐在的矩形,找出C的位置;
(2)根据A的坐标,确定住原点的坐标,从而得出C点的坐标;
(3)根据圆锥与扇形各部分对应情况可以求出;
(4)利用中心对称图形的性质,可以做一个正方形.
(2)根据A的坐标,确定住原点的坐标,从而得出C点的坐标;
(3)根据圆锥与扇形各部分对应情况可以求出;
(4)利用中心对称图形的性质,可以做一个正方形.
解答: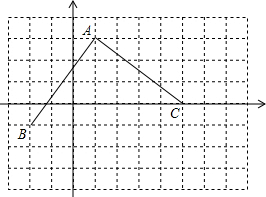 解:(1)点B经过的路径是以点A为圆心,AB长为半径的圆弧;
解:(1)点B经过的路径是以点A为圆心,AB长为半径的圆弧;
(2)∵点A的坐标为(1,3),
∴C点的坐标为:(5,0);
(3)它围成一个几何体的侧面是圆锥形状.
∵n=90°,r=5,
∴扇形的弧长公式:L=
=2πR,
∴
=2πR,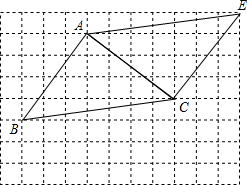
解得:R=1.25;
(4)当AE∥BC,AB∥CE时,四边形ABCE是平行四边形,
∴它是中心对称图形.
 解:(1)点B经过的路径是以点A为圆心,AB长为半径的圆弧;
解:(1)点B经过的路径是以点A为圆心,AB长为半径的圆弧;(2)∵点A的坐标为(1,3),
∴C点的坐标为:(5,0);
(3)它围成一个几何体的侧面是圆锥形状.
∵n=90°,r=5,
∴扇形的弧长公式:L=
| nπr |
| 180 |
∴
| 90×π×5 |
| 180 |

解得:R=1.25;
(4)当AE∥BC,AB∥CE时,四边形ABCE是平行四边形,
∴它是中心对称图形.
点评:此题主要考查了图形的旋转和圆锥与扇形的各部分对应情况以及中心对称图形的性质等知识,此题综合性较强考查知识较多,同学们应特别注意.

练习册系列答案
相关题目
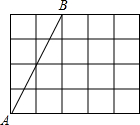 如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )
如图,线段AB的端点是4×5的正方形网格的格点,若再在网格的格点中取一点C,使△ABC成为等腰三角形,则符合条件的点C的个数是( )| A、1个 | B、2个 | C、3个 | D、4个 |
 向旋转90°得到线段AC.
向旋转90°得到线段AC. 33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由).
33、如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由). (2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.
(2010•金东区模拟)如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°.得到线段AC.