题目内容
【题目】如图,△ABC是等边三角形,DE∥AB分别交BC、AC于点D、E,过点E做EF⊥DE,交线段BC的延长线于点F。
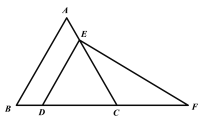
(1)求证:CE=CF;
(2)若BD=![]() CE,AB=8,求线段DF的长。
CE,AB=8,求线段DF的长。
【答案】(1)见解析(2)12
【解析】
(1)根据△ABC是等边三角形得到∠ABC=∠A=∠ACB=60°,根据DE∥AB得到∠DEC=∠EDC=60°,故∠CEF=30°,∠F=90°-∠EDC=30°,则∠F=∠CEF,问题得证;
(2)先证明△DCE为等边三角形,根据BD=![]() CE=
CE=![]() CD,故BD=
CD,故BD=![]() BC,CF=CE=CD=
BC,CF=CE=CD=![]() BC=
BC=![]() AB,故可求解.
AB,故可求解.
(1)∵△ABC是等边三角形
∴∠ABC=∠A=∠ACB=60°,
∵DE∥AB
∴∠DEC=∠EDC=60°,
∵EF⊥DE,
∴∠CEF=90°-∠DEC=30°,∠F=90°-∠EDC=30°,
∴∠F=∠CEF
∴CE=CF
(2)∵∠DEC=∠EDC=60°
∴△DCE为等边三角形,
∵BD=![]() CE=
CE=![]() CD,
CD,
∴BD=![]() BC,
BC,
∴CF=CE=CD=![]() BC=
BC=![]() AB=6,
AB=6,
∴DF=CF+DC=12.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目