题目内容
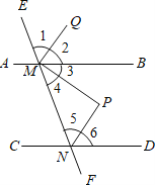
【题目】如图,AB∥CD,直线EF分别与AB,CD相交于M,N,∠AME=60°
(1)求∠DNF的度数;
(2)若∠P=90°,∠2=∠6=60°,求证:MP平分∠BMN.
【答案】(1)∠DNF =60°;(2)见解析
【解析】
(1)利用对顶角相等和两直线平行同位角相等可求;
(2)先利用邻补角互补及已知条件求出∠1=∠5=60°,最后借助平行线及角的和差求出∠3=∠4=30°,即可说明MP平分∠BMN.
解:(1)∵AB∥CD,∠AME=60°,
∴∠CNE=∠AME=60°.
∴∠DNF=∠CNE=60°.
(2)证明:∵∠AME+∠1+∠2=180°,∠DNF+∠5+∠6=180°,
∠2=∠6=60°,∠AME=60°,∠DNF=60°,
∴∠1=∠5=60°,
∴MQ∥NP,
∴∠PMQ=∠P=90°.
∴∠3=∠PMQ-∠2=30°.
∵∠1+∠2+∠3+∠4=∠EMN=180°,
∴∠4=180°-∠1-∠2-∠3=30°.
∴∠3=∠4,
∴MP平分∠BMN.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】某市居民使用自来水按如下标准收费(水费按月缴纳)
月用水量 | 单价 |
不超过 |
|
超过 |
|
超过 |
|
(1)当![]() 时,某用户用了
时,某用户用了![]() 水,求该用户这个月应该缴纳的水费;
水,求该用户这个月应该缴纳的水费;
(2)设某用户用水量为![]() 立方米,求该用户应缴纳的水费(用含
立方米,求该用户应缴纳的水费(用含![]() 的式子表达)
的式子表达)