题目内容
【题目】已知抛物线![]() .
.
(Ⅰ)若抛物线的顶点为![]() (-2,-4),抛物线经过点
(-2,-4),抛物线经过点![]() (-4,0).
(-4,0).
①求该抛物线的解析式;
②连接![]() ,把
,把![]() 所在直线沿
所在直线沿![]() 轴向上平移,使它经过原点
轴向上平移,使它经过原点![]() ,得到直线
,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一动点.
上一动点.
设以点![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的四边形的面积为
为顶点的四边形的面积为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() ≤
≤![]() ≤
≤![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() >0,
>0, ![]() >1,当
>1,当![]() 时,
时, ![]() ,当0<
,当0<![]() <
<![]() 时,
时, ![]() >0,试比较
>0,试比较![]() 与1的大小,并说明理由.
与1的大小,并说明理由.
【答案】(Ⅰ)①该抛物线的解析式为![]() ;②当点
;②当点![]() 在第二象限时,
在第二象限时, ![]() <0,
<0, ![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() ,当点
,当点![]() 在第四象限时,
在第四象限时, ![]() >0,
>0,
![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() ;(Ⅱ)
;(Ⅱ)![]() ≤1.
≤1.
【解析】试题分析:(Ⅰ)①用顶点式即可求出抛物线的解析式;
②首先可以得出直线AB和直线l的解析式.然后分两种情况讨论:①当P在第二象限时,②当P在第四象限时.
(Ⅱ)由当![]() 时,
时, ![]() ,得到
,得到![]() .由
.由![]() 时,
时, ![]() ,知抛物线与
,知抛物线与![]() 轴的一个公共点为(
轴的一个公共点为(![]() ,0).由0<
,0).由0<![]() <
<![]() 时,
时, ![]() >0,知抛物线的对称轴
>0,知抛物线的对称轴![]() ≥
≥![]() ,从而得到
,从而得到 ![]() ≤
≤![]() ,即可得到结论.
,即可得到结论.
试题解析:解:(Ⅰ)①设抛物线的解析式为![]() .
.
∵抛物线经过点![]() (-4,0),∴
(-4,0),∴![]() .解得:
.解得: ![]() ,∴
,∴![]() ,∴该抛物线的解析式为
,∴该抛物线的解析式为![]() .
.
②设直线![]() 的解析式为
的解析式为![]() ,由
,由![]() (-2,-4),
(-2,-4),![]() (-4,0),得:
(-4,0),得: ![]() ,解这个方程组,得:
,解这个方程组,得: ![]() ,∴直线
,∴直线![]() 的解析式为
的解析式为![]() .
.
∵直线![]() 与
与![]() 平行,且过原点,∴直线
平行,且过原点,∴直线![]() 的解析式为
的解析式为![]() .
.
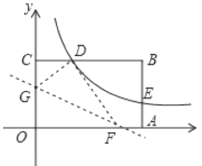
当点![]() 在第二象限时,
在第二象限时, ![]() <0,如图,
<0,如图,
![]() .
. ![]() ,∴
,∴![]() (
(![]() <0).
<0).
∵![]() ≤
≤![]() ≤
≤![]() ,∴
,∴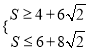 ,即
,即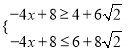 ,
,
解此不等式组,得: ![]() ≤
≤![]() ≤
≤![]() .
.
∴![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() .
.
当点![]() 在第四象限时,
在第四象限时, ![]() >0,过点
>0,过点![]() ,
, ![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
, ![]() ,则:
,则:
![]() ·
·![]() ·
·![]() ·
·![]() .
.
∵![]() ,∴
,∴![]() (
(![]() >0).
>0).
∵![]() ≤
≤![]() ≤
≤![]() ,∴
,∴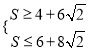 ,即
,即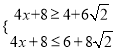 ,
,
解此不等式组,得: ![]() ≤
≤![]() ≤
≤![]() .
.
∴![]() 的取值范围是
的取值范围是![]() ≤
≤![]() ≤
≤![]() .
.
(Ⅱ)∵当![]() 时,
时, ![]() ,∴
,∴![]() .
.
∵![]() >1,∴
>1,∴![]() ,
, ![]() .
.
由![]() 时,
时, ![]() ,知抛物线与
,知抛物线与![]() 轴的一个公共点为(
轴的一个公共点为(![]() ,0).
,0).
把![]() 代入
代入![]() ,得:
,得: ![]() ,∴抛物线与
,∴抛物线与![]() 轴的交点为(0,
轴的交点为(0, ![]() ).
).
由![]() >0知抛物线开口向上,再由0<
>0知抛物线开口向上,再由0<![]() <
<![]() 时,
时, ![]() >0,知抛物线的对称轴
>0,知抛物线的对称轴![]() ≥
≥![]() ,∴
,∴![]() ≤
≤![]() .由
.由![]() 得:
得: ![]() ≤
≤![]() ,∴
,∴![]() ≤1.
≤1.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(辆) | -1 | +3 | -2 | -4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?