Question

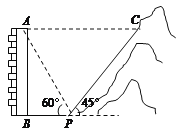
【题目】如图，一居民楼底部B与山脚P位于同一水平线上，小李在P处测得居民楼顶A的仰角为60°，然后他从P处沿坡角为45°的山坡向上走到C处，这时，PC=30 m，点C与点A恰好在同一水平线上，点A、B、P、C在同一平面内．

（1）求居民楼AB的高度；

（2）求C、A之间的距离．（结果保留根号）

Answer 1

【答案】（1）AB=21.2（m）（2）CA=略（注意精确度）

【解析】试题分析：（1）首先分析图形：根据题意构造直角三角形，利用在Rt△CPE中，由sin45°=，得出EC的长度，进而可求出答案．

（2）在Rt△CPE中，tan60°=，得出BP的长，进而得出PE的长，即可得出答案．

试题解析：（1）过点C作CE⊥BP于点E，

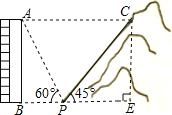
在Rt△CPE中

∵PC=30m，∠CPE=45°，

∴sin45°=，

∴CE=PCsin45°=30× m，

∵点C与点A在同一水平线上，

∴AB=CE=15≈21.2m，

答：居民楼AB的高度约为21.2m；

（2）在Rt△ABP中

∵∠APB=60°，

∴tan60°=，

∴BP=m，

∵PE=CE=15m，

∴AC=BE=15+5≈33.4m，

答：C、A之间的距离约为33.4m．