题目内容
在△ABC中,∠A、∠B、∠C的对边分别用a、b、c表示.
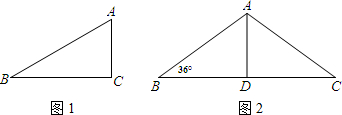
(1)如图1,在△ABC中,∠A=2∠B,∠A=60°,求证:a2=b(b+c);
(2)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.(1)中的三角形是一个特殊的倍角三角形,那么对于任意一个倍角△ABC,且∠A=2∠B,关系式a2=b(b+c)是否仍然成立?请证明你的结论;
(3)在(2)中,若∠B=36°,b=1,直接填空:a=______,cos36°=______(若结果是无理数,请用无理数表示).
(4)应用(3)的结论,解答下面问题:如图2,一厂房屋顶人字架是等腰△ABC,其跨度BC=10m,∠B=∠C=36°,中柱AD⊥BC于D,则上弦AB的长是______m.(可能用到的数: ≈2.24,
≈2.24, ≈2.45,
≈2.45, ≈2.65)
≈2.65)
(1)证明:∵∠A=2∠B,∠A=60°
∴∠B=30°,∠C=90°
∴c=2b,a= b
b
∴a2=3b2=b(b+c).
(2)解:关系式a2=b(b+c)仍然成立.
证明:∵∠A=2∠B
∴∠C=180°-∠A-∠B=180°-3∠B
由正弦定理得 =
= =
= =2R,
=2R,
即a=2RsinA,b=2RsinB,c=2RsinC
∴b(b+c)=2RsinB(2RsinB+2RsinC),
=4R2sinB[sinB+sin(180°-3∠B)]
=4R2sinB(sinB+sin3∠B)
=4R2sinB(2sin2BcosB)
=4R2sin2B×sin2B
=4R2sin22B
又∵a2=4R2sin2A=4R2sin22B
∴a2=b(b+c)
(3)如图所示:
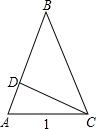
∵a2=b(b+c),a=c,b=1,
∴a= ,
,
设AD=x,则BD= -x,
-x,
则AC2-AD2=BC2-BD2,即1-x2=( )2-(
)2-( -x)2,
-x)2,
解得:x=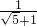 ,BD=
,BD= -
-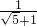 ,
,
故cos36°= =
=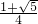 ;
;
(4)由题意得,BD= BC=5m,
BC=5m,
则AB=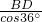 =
=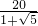 =5(
=5( -1)≈6.2米.
-1)≈6.2米.
分析:(1)根据已知可求得各角的度数,再根据三角函数求得各边的关系,从而不难得到结论.
(2)根据已知表示各角的度数,再根据正弦定理对式子进行整理,从而得到结论;
(3)画出图形,根据a2=b(b+c),a=c,b=1,可求出a,继而可得出cos36°的值.
(4)先求出BD,再由cos36°的值可得出AB.
点评:本题考查了勾股定理、解直角三角形及正弦定理的内容,综合考察的知识点较多,难度较大,解答本题需要同学们能活学活用.
∴∠B=30°,∠C=90°
∴c=2b,a=
 b
b∴a2=3b2=b(b+c).
(2)解:关系式a2=b(b+c)仍然成立.
证明:∵∠A=2∠B
∴∠C=180°-∠A-∠B=180°-3∠B
由正弦定理得
 =
= =
= =2R,
=2R,即a=2RsinA,b=2RsinB,c=2RsinC
∴b(b+c)=2RsinB(2RsinB+2RsinC),
=4R2sinB[sinB+sin(180°-3∠B)]
=4R2sinB(sinB+sin3∠B)
=4R2sinB(2sin2BcosB)
=4R2sin2B×sin2B
=4R2sin22B
又∵a2=4R2sin2A=4R2sin22B
∴a2=b(b+c)
(3)如图所示:
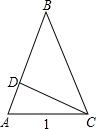
∵a2=b(b+c),a=c,b=1,
∴a=
 ,
,设AD=x,则BD=
 -x,
-x,则AC2-AD2=BC2-BD2,即1-x2=(
 )2-(
)2-( -x)2,
-x)2,解得:x=
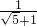 ,BD=
,BD= -
-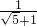 ,
,故cos36°=
 =
=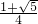 ;
;(4)由题意得,BD=
 BC=5m,
BC=5m,则AB=
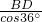 =
=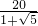 =5(
=5( -1)≈6.2米.
-1)≈6.2米.分析:(1)根据已知可求得各角的度数,再根据三角函数求得各边的关系,从而不难得到结论.
(2)根据已知表示各角的度数,再根据正弦定理对式子进行整理,从而得到结论;
(3)画出图形,根据a2=b(b+c),a=c,b=1,可求出a,继而可得出cos36°的值.
(4)先求出BD,再由cos36°的值可得出AB.
点评:本题考查了勾股定理、解直角三角形及正弦定理的内容,综合考察的知识点较多,难度较大,解答本题需要同学们能活学活用.

练习册系列答案
相关题目
在△ABC中,∠C=90°,BC=12,AB=13,则tanA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,a=
,b=
,c=2
,则最大边上的中线长为( )
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于