Question

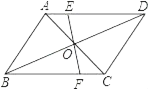
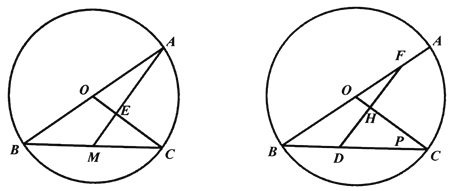
【题目】如图已知：AB是圆O的直径，AB=10，点C为圆O上异于点A、B的一点，点M为弦BC的中点．

（1）如果AM交OC于点E，求OE：CE的值；

（2）如果AM⊥OC于点E，求∠ABC的正弦值；

（3）如果AB：BC=5：4，D为BC上一动点，过D作DF⊥OC，交OC于点H，与射线BO交于圆内点F，请完成下列探究．

探究一：设BD=x，FO=y，求y关于x的函数解析式及其定义域．

探究二：如果点D在以O为圆心，OF为半径的圆上，写出此时BD的长度．

Answer 1

【答案】（1）OE:CE=1：2；（2）；（3）探究一： （其中），探究二：.

【解析】

（1）过点O作ON║BC交AM于点N，根据AB是圆O的直径，点M为弦BC的中点即可；

（2）证明△OME∽△MCE，求出即可；

（3）过点D作DL⊥BO于点L，设BD=，则CD=，BL=DL=，CH=，OH= ，根据，求出y的解析式，再根据OC垂直平分DF，求出BD即可.

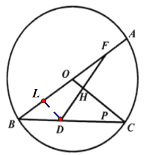
解：（1）过点O作ON║BC交AM于点N，

∵AB是圆O的直径，ON∥BM，∴

∵点M为弦BC的中点，∴

∴OE:CE=ON:BM=1：2

（2）∵点M为弦BC的中点，

∴OM⊥BC.

∴∠C＋∠MOC=90°，

∵AM⊥OC于点E，

∴∠MOC＋∠OME=90°，

∴∠OME=∠C.

∵∠OME=∠C，∠MOE=∠MOE，

∴△OME∽△MCE

∴.

设OE=，则CE=2， ME=

在直角△MCE中，，

∴.

（3）过点D作DL⊥BO于点L，

∵AB=10，AB：BC=5：4，

∴BC=8，

设BD=，则CD=，BL=DL=，CH=，OH= ，

∵OH∥LD，

∴

∴

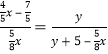
∴ （其中）

∵以O为圆心，OF为半径的圆经过D，

∴OC垂直平分DF，FO=OL，

，

此时．