题目内容
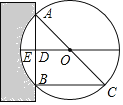
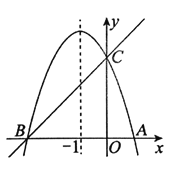
【题目】如图,已知对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于C点,其中
轴交于C点,其中![]() .
.
(1)求点B的坐标及此抛物线的表达式;
(2)点D为y轴上一点,若直线BD和直线BC的夹角为15,求线段CD的长度;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,当
上的一个动点,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)CD=
;(2)CD=![]() 或
或![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将A、C坐标代入抛物线,结合抛物线的对称轴,解得a、b、c的值,求得抛物线解析式;
(2)求出直线BC的解析式为![]() ,得出∠CBA=45°再求出∠DBA=30°或∠DBA=60°,再求出DO即可;
,得出∠CBA=45°再求出∠DBA=30°或∠DBA=60°,再求出DO即可;
(3)设点P的坐标,分别以B、C、P为直角顶点,进行分类讨论,再运用勾股定理得到方程式进行求解.
解:(1)根据对称轴x=-1,A(1,0),得出B为(-3,0)
依题意得: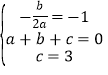 ,解之得:
,解之得: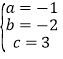 ,
,
∴抛物线的解析式为![]() .
.
(2)∵对称轴为![]() ,且抛物线经过
,且抛物线经过![]() ,∴
,∴![]()
∴直线BC的解析式为![]() . ∠CBA=45°
. ∠CBA=45°
∵直线BD和直线BC的夹角为15, ∴∠DBA=30°或∠DBA=60°
在△BOD,![]() ,BO=3
,BO=3
∴DO=![]() 或
或![]() ,∴CD=
,∴CD=![]() 或
或![]() .
.
(3)设![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,,
,,
①若点![]() 为直角顶点,则
为直角顶点,则![]() 即:
即:![]() 解之得:
解之得:![]() ,
,
②若点![]() 为直角顶点,则
为直角顶点,则![]() 即:
即:![]() 解之得:
解之得:![]() ,
,
③若点![]() 为直角顶点,则
为直角顶点,则![]() 即:解之得:
即:解之得:![]()
![]() ,
,![]() .
.
综上所述![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目