题目内容
【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
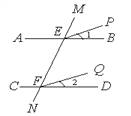
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
【答案】 两直线平行,同位角相等 MFQ FQ 同位角相等地,两直线平行
【解析】试题分析:由AB与CD平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,利用等式的性质得到一对同位角相等,可得出EP与FQ平行.
试题解析:证明:∵AB∥CD,
∴∠MEB=∠MFD(两直线平行同位角相等),
又∵∠1=∠2(已知),
∴∠MEB∠1=∠MFD∠2,
即∠MEP=∠MFQ,
∴EP∥FQ(同位角相等两直线平行).
故答案为:两直线平行同位角相等;已知;MFQ;FQ;同位角相等两直线平行.

练习册系列答案
相关题目
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯 | 电量 | 电价 |
一档 | 0~180度 | 0.6元/度 |
二档 | 181~400度 | 二档电价 |
三档 | 401度及以上 | 三档电价 |