题目内容
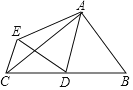
【题目】已知,△ABC是等边三角形,如图①,点D、E分别在射线BA、BC上,且AD=CE,求证:△BDE是等边三角形;

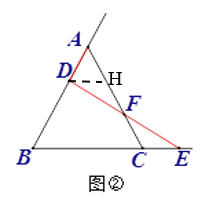
(2)如图②,点D在BA边上,点E在射线BC上,AD=CE,连接DE交AC于点F,请问DF与EF的数量关系是什么?并说明理由.
【答案】(1)见解析;(2)DF=EF,理由见解析.
【解析】
(1)利用有一个角是60度的等腰三角形是等边三角形进行判定;
(2)过点D作DH∥BE交AC于点H,证得△DHF≌△ECF(ASA),可得出DF=EF.
(1)证明:∵△ABC是等边三角形,
∴∠B =60°,AB=BC,
∵AD=CE,
∴AB+AD=BC+CE,即BD=BE,
∴△BDE是等腰三角形,
又∵∠B =60°,
∴△BDE是等边三角形;
(2)DF=EF,理由是:
如图②,过点D作DH∥BE交AC于点H,
∵△ABC是等边三角形,
∴∠A=∠B =∠ACB=60°,
∵DH∥BE,
∴∠ADH=∠B =60°,∠AHD=∠ACB =60°,
∴△ADH是等边三角形,
∴AD=DH,
∵AD=CE,
∴DH=CE,
∵DH∥BE,
∴∠HDF=∠E, ∠DHF=∠FCE,
在△DHF和△ECF中,
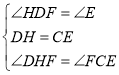
∴△DHF≌△ECF(ASA)
∴DF=EF

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中,x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 |
y | 0 | ﹣3 | ﹣4 | ﹣3 |
下列结论:
①ac<0;
②当x>1时,y随x的增大而增大;
③﹣4是方程ax2+(b﹣4)x+c=0的一个根;
④当﹣1<x<0时,ax2+(b﹣1)x+c+3>0.其中正确结论的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个