题目内容
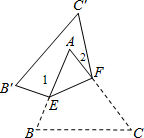
如图，把△ABC纸片沿DE折叠，当点A落在四边形BCED内部时，∠B+∠C可由∠1，∠2表示为（ ）
| A．∠B+∠C=180°-∠1-∠2 | B．∠B+∠C=180°-
| ||
| C．∠B+∠C=90°+∠1+∠2 | D．无法表示 |
∵∠A+∠A+∠AEA′+∠ADA′=360°
又∵∠1+∠AEA′+∠2+∠ADA′=360°，
∴∠A+∠A′=∠1+∠2，
又∵∠A=∠A′，
∴2∠A′=∠1+∠2，即∠1+∠2=360°-2（∠B+∠C），
∴∠B+∠C=180°-
．
故选：B．
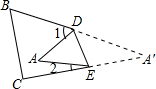
又∵∠1+∠AEA′+∠2+∠ADA′=360°，
∴∠A+∠A′=∠1+∠2，
又∵∠A=∠A′，
∴2∠A′=∠1+∠2，即∠1+∠2=360°-2（∠B+∠C），
∴∠B+∠C=180°-
| ∠1+∠2 |
| 2 |
故选：B．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
