题目内容
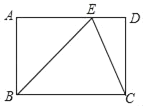
【题目】菱形ABCD中,∠B=60°,AB=4,点E在BC上,CE=2![]() ,若点P是菱形上异于点E的另一点,CE=CP,则EP的长为_____.
,若点P是菱形上异于点E的另一点,CE=CP,则EP的长为_____.
【答案】6或2![]() 或3
或3![]() ﹣
﹣![]() .
.
【解析】
连接EP交AC于点H,依据菱形的性质可得到∠ECH=∠PCH=60°,然后依据SAS可证明△ECH≌△PCH,则∠EHC=∠PHC=90°,最后依据PE=EH求解即可.
解:如图所示:连接EP交AC于点H.

∵菱形ABCD中,∠B=60°,
∴∠BCD=120°,∠ECH=∠PCH=60°.
在△ECH和△PCH中 ,
,
∴△ECH≌△PCH.
∴∠EHC=∠PHC=90°,EH=PH.
∴OC=![]() EC=
EC=![]() .
.
∴EH=3,
∴EP=2EH=6.
如图2所示:当P在AD边上时,△ECP为等腰直角三角形,则![]() .
.

当P′在AB边上时,过点P′作P′F⊥BC.
∵P′C=2![]() ,BC=4,∠B=60°,
,BC=4,∠B=60°,
∴P′C⊥AB.
∴∠BCP′=30°.
∴![]() .
.
∴![]() .
.
故答案为6或2![]() 或3
或3![]() ﹣
﹣![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】某电子厂一周计划生产700台相同型号的电子玩具,平均每天生产100台,由于各种原因实际每天生产量与计划量相比有出入(超过为正,不足为负,单位:台),下表是某周每天的生产情况
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
产量 | +5 | -3 | -4 | +10 | -6 | +12 | -7 |
(1)根据记录可知前三天共生产______台;
(2)产量最多的一天比产量最少的一天多生产______台;
(3)该厂实行计件工资制,每生产一台电子玩具40元,若按周计算,超额完成任务,超出部分每台50元;若未完成任务,生产出的电子玩具每台只能按35元发工资.那么该厂工人这一周的工资总额是多少?
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)