题目内容
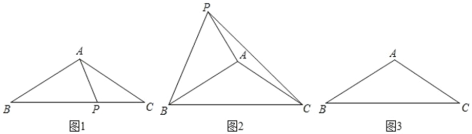
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将ΔADP沿AP翻折得到![]() ,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
,PD′的延长线交边AB于点M,过点B作BN‖MP交DC于点N.
图1
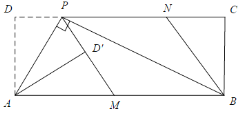
图2
(1)求证:![]() ;
;
(2)请判断四边形PMBN的形状,并说明理由;
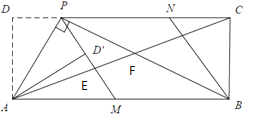
(3)如图2,连接AC,分别交PM,PB于点E,F.若tan∠PAD=![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)是菱形;(3)![]()
【解析】
(1)要证明![]() ,就需证明
,就需证明![]() =
=![]() ,根据矩形ABCD可知AD=BC,
,根据矩形ABCD可知AD=BC,
因此需要证明![]() =
=![]() ,即需要证明△ADP∽△PCB相似,
,即需要证明△ADP∽△PCB相似,
根据矩形![]() 可知
可知![]() ,
,
在![]() 中,可得
中,可得![]() ,
,
再由![]() ,
,![]() 可知,
可知,![]() ,从而得到
,从而得到![]() ,
,
即可以根据“两角相等的两个三角形相似”来证明![]() 和
和![]() 相似。
相似。
(2)观察图形可发现四边形![]() 是菱形,
是菱形,
根据“一组邻边相等的平行四边形是菱形”可知,需要先证明四边形![]() 是平行四边形,再证明其中一组邻边相等,由
是平行四边形,再证明其中一组邻边相等,由![]() ,
,![]() ,根据“两组对边分别平行的四边形是平行四边形”即可证明四边形
,根据“两组对边分别平行的四边形是平行四边形”即可证明四边形![]() 是平行四边形,
是平行四边形,
由翻折形成的两个全等三角形![]() 和
和![]() 得出
得出![]() ,
,
进而根据![]() ,
,![]() ,得出
,得出![]() ,
,
再由![]() ,得到内错角
,得到内错角![]() 相等,等量代换为
相等,等量代换为![]() ,
,
根据“等角对等边”得出邻边![]() 和
和![]() 相等,从而说明四边形
相等,从而说明四边形![]() 是菱形。
是菱形。
(1)证明:∵![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 。
。
(2)四边形![]() 是菱形。
是菱形。
证明:因为![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() (翻折),
(翻折),
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
于是![]() ,
,
∴![]() ,
,
又∵四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是菱形。
是菱形。
(3)(3)设![]() (
(![]() ),
),
∵在Rt△APDA中,tan∠PAD=![]()
∴![]() ,所以
,所以![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 为矩形,
为矩形,
∴![]() ,
,![]() ,
,
∵![]() (翻折),
(翻折),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
于是![]() ,
,
∴![]() ,
,
∵![]() ,
,
所以![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,即CF=
,即CF=![]() AC
AC
∵![]() ,
,![]() (对顶角),
(对顶角),
∴![]() ,
,
∴![]() ,
,
∴![]() ,即AE=
,即AE=![]() AC
AC
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目