题目内容
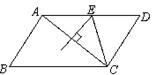
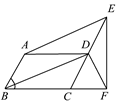
如图，平行四边形ABCD中，∠ABC＝60°，E、F分别在CD、BC的延长线上，AE∥BD，EF⊥BC，DF＝2，则EF的长为( )
A．2
B．2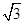
C．4
D．4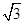
A．2
B．2
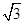
C．4
D．4
B
本题考查平行四边形的性质的运用
由平行四边形的性质及直角三角形的性质，推出△CDF为等边三角形，再根据勾股定理解答即可．
∵AB∥CD，
∴∠DCF=60°，
又∵EF⊥BC，
∴∠CEF=30°，
∴
，
又∵AE∥BD，
∴AB=CD=DE，
∴CF=CD，
又∵∠DCF=60°，
∴∠CDF=∠DFC=60°，
∴CD=CF=DF=DE=2，
故选B.
由平行四边形的性质及直角三角形的性质，推出△CDF为等边三角形，再根据勾股定理解答即可．
∵AB∥CD，
∴∠DCF=60°，
又∵EF⊥BC，
∴∠CEF=30°，
∴
，又∵AE∥BD，
∴AB=CD=DE，
∴CF=CD，
又∵∠DCF=60°，
∴∠CDF=∠DFC=60°，
∴CD=CF=DF=DE=2，
故选B.
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
自B→A→E→B停止，点Q自D→F→C→D停止，点P运动的路程是m，点Q运动的路程是n，当四边形BPDQ是平行四边形时，求m与n满足的数量关系．(画出示意图)
