题目内容
如图①E、F、G、H为正方形ABCD各边延长线上的点,CE=BC,DF=CD,AG=DA,BH=AB,若正方形ABCD的面积等于1.(1)请你求出四边形EFGH的面积;
(2)如图②,图③,若将正方形ABCD变为矩形和菱形,其他条件仍然不变,请你分别写出四边形EFGH的面积.
(3)如图④,若将正方形ABCD变为任意四边形,其他条件仍然不变,请你猜想四边形EFGH的面积并说明理由.
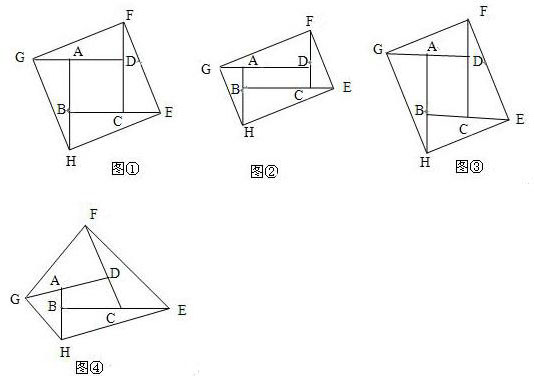
分析:(1)依题意已知四边形ABCD的面积为1,可推出BH=BC=1,求得BE=2,S△BEH=1,故同理证得S△AGH=S△DGF=S△FCE=S△BEH=1,故四边形面积为四个三角形以及一个四边形的和为5;
(2)依题意可知矩形ABCD的面积为1,其余四个三角形可证明其两两全等,然后根据(1)的证明方法可证得四边形EFGH的面积为5;
(3)依题意可知CE=BC,DF=CD,AG=DA,BH=AB,可证得四个三角形的面积相等,从而得出四边形的面积.
(2)依题意可知矩形ABCD的面积为1,其余四个三角形可证明其两两全等,然后根据(1)的证明方法可证得四边形EFGH的面积为5;
(3)依题意可知CE=BC,DF=CD,AG=DA,BH=AB,可证得四个三角形的面积相等,从而得出四边形的面积.
解答:解:(1)∵四边形ABCD的面积等于1,
∴BH=BC=1,
∴BE=2,
∴S△BEH=1,
同理S△AGH=S△DGF=S△FCE=S△BEH=1,
∴四边形EFGH的面积为5;
(2)∵矩形ABCD的面积为1,
∴CD•BC=1,
∵CE=BC,DF=CD,
∴S△ECF=
CE•CF=
CD•2BC=1,
同理S△AGH=S△DGF=S△FCE=S△BEH=1,
∴四边形EFGH的面积均为5;
(3)依题意可知CE=BC,DF=CD,AG=DA,BH=AB,
故S△AGH=S△DGF=S△FCE=S△BEH=1
所以四边形面积仍为5.
∴BH=BC=1,
∴BE=2,
∴S△BEH=1,
同理S△AGH=S△DGF=S△FCE=S△BEH=1,
∴四边形EFGH的面积为5;
(2)∵矩形ABCD的面积为1,
∴CD•BC=1,
∵CE=BC,DF=CD,
∴S△ECF=
| 1 |
| 2 |
| 1 |
| 2 |
同理S△AGH=S△DGF=S△FCE=S△BEH=1,
∴四边形EFGH的面积均为5;
(3)依题意可知CE=BC,DF=CD,AG=DA,BH=AB,
故S△AGH=S△DGF=S△FCE=S△BEH=1
所以四边形面积仍为5.
点评:本题考查的是正方形的性质,考生注意总结规律解答题目.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
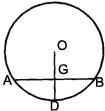 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=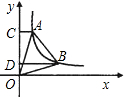 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

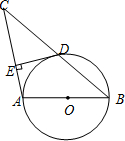 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.