题目内容
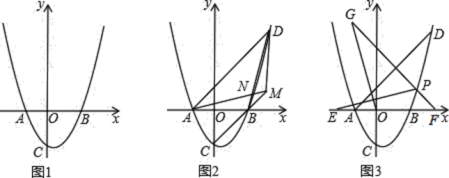
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 的顶点是A(1,3),将OA绕点O逆时针旋转
的顶点是A(1,3),将OA绕点O逆时针旋转![]() 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.

(1)求抛物线的解析式;
(2)P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与![]() 的边分别交于M,N两点,将
的边分别交于M,N两点,将![]() 以直线MN为对称轴翻折,得到
以直线MN为对称轴翻折,得到![]() .
.
设点P的纵坐标为m.
①当![]() 在
在![]() 内部时,求m的取值范围;
内部时,求m的取值范围;
②是否存在点P,使![]() ,若存在,求出满足m的值;若不存在,请说明理由.
,若存在,求出满足m的值;若不存在,请说明理由.
【答案】![]() ;(2)①
;(2)①![]() ;②存在,满足m的值为
;②存在,满足m的值为![]() 或
或![]() .
.
【解析】
(1)作AD⊥y轴于点D,作BE⊥x轴于点E,然后证明△AOD≌△BOE,则AD=BE,OD=OE,即可得到点B的坐标,然后利用待定系数法,即可求出解析式;
(2)①由点P为线段AC上的动点,则讨论动点的位置是解题的突破口,有点P与点A重合时;点P与点C重合时,两种情况进行分析计算,即可得到答案;
②根据题意,可分为两种情况进行当点M在线段OA上,点N在AB上时;当点M在线段OB上,点N在AB上时;先求出直线OA和直线AB的解析式,然后利用m的式子表示出两个三角形的面积,根据等量关系列出方程,解方程即可求出m的值.
解:(1)如图:作AD⊥y轴于点D,作BE⊥x轴于点E,

∴∠ADO=∠BEO=90°,
∵将OA绕点O逆时针旋转![]() 后得到OB,
后得到OB,
∴OA=OB,∠AOB=90°,
∴∠AOD+∠AOE=∠BOE+∠AOE=90°,
∴∠AOD=∠BOE,
∴△AOD≌△BOE,
∴AD=BE,OD=OE,
∵顶点A为(1,3),
∴AD=BE=1,OD=OE=3,
∴点B的坐标为(3,![]() ),
),
设抛物线的解析式为![]() ,
,
把点B代入,得
![]() ,
,
∴![]() ,
,
∴抛物线的解析式为![]() ,
,
即![]() ;
;
(2)①∵P是线段AC上一动点,
∴![]() ,
,
∵当![]() 在
在![]() 内部时,
内部时,
当点![]() 恰好与点C重合时,如图:
恰好与点C重合时,如图:

∵点B为(3,![]() ),
),
∴直线OB的解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴点C的坐标为(1,![]() ),
),
∴AC=![]() ,
,
∵P为AC的中点,
∴AP=![]() ,
,
∴![]() ,
,
∴m的取值范围是![]() ;
;
②当点M在线段OA上,点N在AB上时,如图:

∵点P在线段AC上,则点P为(1,m),
∵点![]() 与点A关于MN对称,则点
与点A关于MN对称,则点![]() 的坐标为(1,2m
的坐标为(1,2m![]() 3),
3),
∴![]() ,
,![]() ,
,
设直接OA为![]() ,直线AB为
,直线AB为![]() ,
,
分别把点A,点B代入计算,得
直接OA为![]() ;直线AB为
;直线AB为![]() ,
,
令![]() ,
,
则点M的横坐标为![]() ,点N的横坐标为
,点N的横坐标为![]() ,
,
∴![]() ;
;
∵![]() ;
;
![]() ;
;
又∵![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
当点M在边OB上,点N在边AB上时,如图:

把![]() 代入
代入![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() 或
或![]() (舍去);
(舍去);
综合上述,m的值为:![]() 或
或![]() .
.