题目内容
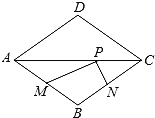
【题目】如图,菱形ABCD的两条对角线分别长6和8,点P是对角统AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是（ ）
A. 10 B. 8 C. 5 D. 4
【答案】C
【解析】
作ME⊥AC交AD于E，连接EN，则EN就是PM+PN的最小值，再证明四边形ABNE是平行四边形，利用联系单性质及勾股定理求得AB的长，由此即可求得EN的长，问题得解.
如图：作ME⊥AC交AD于E，连接EN，则EN就是PM+PN的最小值，
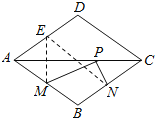
∵M、N分别是AB、BC的中点，
∴BN=BM=AM，
∵ME⊥AC交AD于E，
∴AE=AM，
∴AE=BN，AE∥BN，
∴四边形ABNE是平行四边形，
∴EN=AB，EN∥AB，
而由题意可知，可得AB=
=5，
∴EN=AB=5，
∴PM+PN的最小值为5．
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
