ЬтФПФкШн
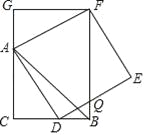
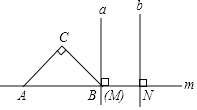
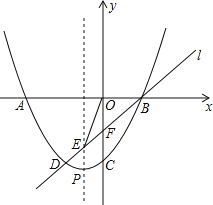
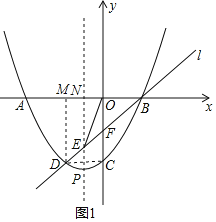
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНax2+2ax+cЃЈaЃО0ЃЉЕФЭМЯѓНЛxжсгкAЁЂBСНЕуЃЌНЛyжсгкЕуCЃЎЙ§ЕуBЕФжБЯпlгыетИіЖўДЮКЏЪ§ЕФЭМЯѓЕФСэвЛИіНЛЕуЮЊDЃЌгыИУЭМЯѓЕФЖдГЦжсНЛгкЕуEЃЌгыyжсНЛгкЕуFЃЌЧвDEЃКEFЃКFBЃН1ЃК1ЃК2ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЕуFЮЊOCЕФжаЕуЃЛ
ЃЈ2ЃЉСЌНгOEЃЌШєЁїOBEЕФУцЛ§ЮЊ2ЃЌЧѓетИіЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉЩшетИіЖўДЮКЏЪ§ЕФЭМЯѓЕФЖЅЕуЮЊPЃЌЮЪЃКвдDFЮЊжБОЖЕФдВЪЧЗёПЩФмЧЁКУОЙ§ЕуPЃПШєПЩФмЃЌЧыЧѓГіДЫЪБЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛШєВЛПЩФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉвдDFЮЊжБОЖЕФдВФмЙЛЧЁКУОЙ§ЕуPЃЌ
ЃЛЃЈ3ЃЉвдDFЮЊжБОЖЕФдВФмЙЛЧЁКУОЙ§ЕуPЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЪзЯШЕУГіЖдГЦжсЃЌдйБэЪОГіDЃЌCЕузјБъЃЌдйРћгУШЋЕШШ§НЧаЮЕФХаЖЈЗНЗЈЕУГіЁїDCFЁеЁїBOFЃЌНјЖјЧѓГіД№АИЃЛ
ЃЈ2ЃЉЪзЯШЕУГіFЕузјБъЃЌНјЖјРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпBCЕФНтЮіЪНЃЌНјЖјЕУГіД№АИЃЛ
ЃЈ3ЃЉгЩЃЈ1ЃЉПЩЕУFЃЈ0ЃЌ![]() ЃЉЃЌEЃЈЉ1ЃЌ
ЃЉЃЌEЃЈЉ1ЃЌ![]() ЃЉЃЌдйРћгУEPЃНDEЃЌНјЖјЕУГіЙигкaЃЌcЕФЕШЪНЃЌНјЖјЧѓГіД№АИЃЎ
ЃЉЃЌдйРћгУEPЃНDEЃЌНјЖјЕУГіЙигкaЃЌcЕФЕШЪНЃЌНјЖјЧѓГіД№АИЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЙ§ЕуDзїDMЁЮFOЃЌ
ЁпyЃНax2+2ax+cЃНaЃЈx+1ЃЉ2+cЉaЃЌ
ЁрЫќЕФЖдГЦжсЮЊxЃНЉ1ЃЌ
ЁпDEЃКEFЃКFBЃН1ЃК1ЃК2ЃЌЧвDMЁЮNEЁЮOFЃЌ
ЁрBЃЈ2ЃЌ0ЃЉЃЌЧвDЕуЕФКсзјБъЮЊЉ2ЃЌ
гЩДЫПЩЕУDЃЈЉ2ЃЌcЃЉЃЌ
ЁпЕуCЃЈ0ЃЌcЃЉЃЌ
ЁрDЁЂCЙигкxЃНЉ1ЖдГЦЃЌ
ЙЪЁЯDCFЃН90ЁуЃЌ
дкЁїDCFКЭЁїBOFжа
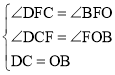
ЁрЁїDCFЁеЁїBOFЃЌ
ЁрOFЃНCFЃЌ
МДЕуFЮЊCOЕФжаЕуЃЎ
ЃЈ2ЃЉЁпЁїOBEЕФУцЛ§ЮЊ2ЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЁрEЃЈЉ1ЃЌЉ2ЃЉЃЌ
ЁпOFЁЮNEЃЌ
ЁрЁїBOFЁзЁїBNEЃЌ
Ёр![]()
Ёр![]()
НтЕУЃКFOЃН![]() ЃЌ
ЃЌ
гЩДЫПЩЕУFЃЈ0ЃЌЉ![]() ЃЉЃЌCЃЈ0ЃЌЉ
ЃЉЃЌCЃЈ0ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
АбBЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ![]() ЃЉДњШыyЃНax2+2ax+cЕУ
ЃЉДњШыyЃНax2+2ax+cЕУ
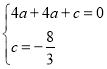
НтЕУЃК 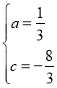
ЁрХзЮяЯпНтЮіЪНЮЊЃК ![]()
ЃЈ3ЃЉвдDFЮЊжБОЖЕФдВФмЙЛЧЁКУОЙ§ЕуPЃЌ
гЩЃЈ1ЃЉПЩЕУFЃЈ0ЃЌ![]() ЃЉЃЌEЃЈЉ1ЃЌ
ЃЉЃЌEЃЈЉ1ЃЌ![]() ЃЉЃЌDЃЈЉ2ЃЌcЃЉЃЌ
ЃЉЃЌDЃЈЉ2ЃЌcЃЉЃЌ
Ёр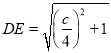
вЊЪЙвдDFЮЊжБОЖЕФдВЧЁКУОЙ§ЕуPЃЌгаEPЃН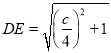
ЁпEЃЈЉ1ЃЌ![]() ЃЉЃЌPЃЈЉ1ЃЌcЉaЃЉЃЌ
ЃЉЃЌPЃЈЉ1ЃЌcЉaЃЉЃЌ
ЁрEPЃН![]()
Ёр
СэвЛЗНУцЃЌгЩBЃЈ2ЃЌ0ЃЉПЩЕУ8a+cЃН0ЃЌМДcЃНЉ8aЃЌ
АбЫќДњШыЩЯЪНПЩЕУaЃН![]() ЃЌ
ЃЌ
Ёр![]()

ЁОЬтФПЁПЕкЪЎЖўНьаЃдАвеЪѕНке§дкШчЛ№ШчнБЕФНјааЃЌЮваЃОХФъМЖзщжЏ1500УћбЇЩњВЮМгСЫвЛДЮЁАЯцвЛЧщаЃдАжЊЪЖЁБДѓШќЃЎШќКѓЗЂЯжЫљгаВЮШќбЇЩњЕФГЩМЈОљВЛЕЭгк60ЗжЃЌЮЊСЫИќКУЕиСЫНтБОДЮДѓШќЕФГЩМЈЗжВМЧщПіЃЌЫцЛњГщШЁСЫЦфжаШєИЩУћбЇЩњЕФГЩМЈзїЮЊбљБОЃЌГЩМЈШчЯТЃК
90ЃЌ92ЃЌ81ЃЌ82ЃЌ78ЃЌ95ЃЌ86ЃЌ88ЃЌ72ЃЌ66ЃЌ62ЃЌ68ЃЌ89ЃЌ86ЃЌ93ЃЌ97ЃЌ100ЃЌ73ЃЌ76ЃЌ80ЃЌ77ЃЌ81ЃЌ86ЃЌ89ЃЌ82ЃЌ85ЃЌ71ЃЌ68ЃЌ74ЃЌ98ЃЌ90ЃЌ97ЃЌ100ЃЌ84ЃЌ87ЃЌ73ЃЌ65ЃЌ92ЃЌ96ЃЌ60ЃЎ
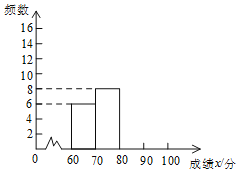
ЖдЩЯЪіГЩМЈНјааСЫећРэЃЌЕУЕНЯТСаВЛЭъећЕФЭГМЦЭМБэЃК
ГЩМЈx/Зж | ЦЕЪ§ | ЦЕТЪ |
60ЁмxЃМ70 | 6 | 0.15 |
70ЁмxЃМ80 | 8 | 0.2 |
80ЁмxЃМ90 | a | b |
90ЁмxЁм100 | c | d |
ЧыИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉaЃНЁЁ ЁЁЃЌbЃНЁЁ ЁЁЃЌcЃНЁЁ ЁЁЃЌdЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈАќРЈ90ЗжЃЉЕФЮЊЁАгХЁБЕШЃЌЧыФуЙРМЦВЮМгетДЮБШШќЕФ1500УћбЇЩњжаГЩМЈЁАгХЁБЕШЕФдМгаЖрЩйШЫЃП