题目内容
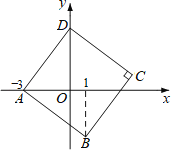
【题目】在平面直角坐标系xOy中,A(0,4),B(2,0),C(5,1),D(2,5).

(1)AD= ,AB= ;
(2)∠BAD是直角吗?请说出理由;
(3)求点B到直线CD的距离.
【答案】(1)![]() ,2
,2![]() ;(2)∠BAD是直角,见解析;(3)点B到直线CD的距离为3.
;(2)∠BAD是直角,见解析;(3)点B到直线CD的距离为3.
【解析】
(1)直接根据两点间的距离公式可求出AD及AB的长即可;
(2)连接BD,根据勾股定理的逆定理进行判断即可;
(3)过点B作BE⊥CD于点E,作CG⊥x轴于点G,根据三角形的面积公式求出BE的长即可.
解:(1)∵A(0,4),B(2,0),C(5,1),D(2,5).
∴AD=![]() =
=![]() ;
;
AB=![]() =
=![]() =2
=2![]() .
.
故答案为:![]() ,2
,2![]() ;
;
(2)∠BAD是直角.
理由:连接BD,
∵B(2,0),D(2,5),
∴BD=5﹣0=5.
∵由(1)知AD=![]() ,AB=2
,AB=2![]() ,
,
∴AD2=5,AB2=20,BD2=25,
∴AD2+AB2=BD2,
∴∠BAD是直角;
(3)过点B作BE⊥CD于点E,作CG⊥x轴于点G,
∵C(5,1),D(2,5),
∴CD=![]() =5,
=5,
∵B(2,0),D(2,5).
∴BD⊥x轴,BG=5﹣2=3,CG=1,
∴S△BCD=S梯形DBGC﹣S△BCG,即![]() ×5BE=
×5BE=![]() (1+5)×3﹣
(1+5)×3﹣![]() ×1×3,解得BE=3.
×1×3,解得BE=3.
答:点B到直线CD的距离为3.

练习册系列答案
相关题目