题目内容
【题目】如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(﹣3,0),B(1,b),则正方形ABCD的面积为( )
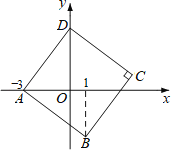
A.34B.25C.20D.16
【答案】B
【解析】
作BE⊥x轴于E,如图,证明△ADO≌△BAE得到OD=AE=4,然后利用勾股定理计算出AD2,从而得到正方形ABCD的面积.
解:作BE⊥x轴于E,如图,
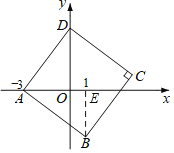
∵A(﹣3,0),B(1,b),
∴AE=4,
∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∵∠DAO+∠BAE=90°,∠DAO+∠ADO=90°,
∴∠ADO=∠BAE,
在△ADO和△BAE中 ,
,
∴△ADO≌△BAE,
∴OD=AE=4,
在Rt△AOD中,AD2=32+42=52=25,
∴正方形ABCD的面积为25.
故选:B.

练习册系列答案
相关题目