题目内容
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
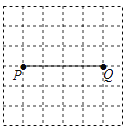
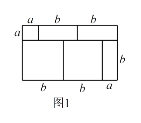
(1)在图1中画出一个面积最小的¨PAQB;
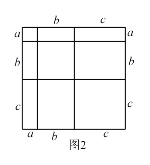
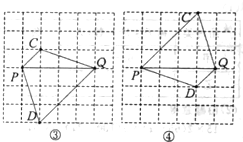
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
【答案】(1)画图见解析;(2)画图见解析.
【解析】
分析: (1)此题是开放性的命题,利用方格纸的特点及几何图形的面积计算方法割补法,把四边形PAQB的面积转化为三角形APQ,与三角形PBQ两个三角形的面积之和,而每个三角形都选择PQ为底,根据底一定,要使面积最小,则满足高最小,且同时满足顶点在格点上上即可;
(2)根据题意,画出的四边形是轴对称图形,不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.故可知此四边形是等腰梯形,根据方格纸的特点,作出满足条件的图形即可.
详解:
(1)
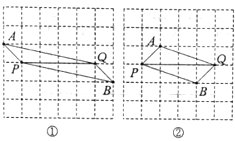
(2)

练习册系列答案
相关题目