题目内容
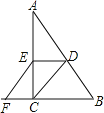
【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
【答案】(1)见解析;(2)4cm.
【解析】
(1)根据三角形中位线定理可得ED∥FC;结合已知条件EF∥DC,即可得结论;
(2)根据直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC.
(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC=![]() AB,
AB,
∴AB=2DC=4cm.
故答案为:(1)见解析;(2)4cm.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目