题目内容
 如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13
如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13(1)求四边形BOAD的面积;
(2)求点D的坐标.
分析:(1)连接AB,则在RT△OAB中,利用勾股定理可求出AB,继而利用勾股定理的逆定理可判断出△ABD也是直角三角形,根据S四边形BOAD=S△AOB+S△ABD即可得出答案.
(2)设则根据DA及DB的长度可得出x、y的值,继而得出点B坐标.
(2)设则根据DA及DB的长度可得出x、y的值,继而得出点B坐标.
解答:解:(1)连接AB,则AB2=OA2+OB2=25,

又∵DB=12,DA=13,
∴DA2=DB2+AB2,
∴△ABD是直角三角形,
故S四边形BOAD=S△AOB+S△ABD=
×3×4+
×5×12=36;
(2)过点D作DE⊥OA,过点B作BF⊥DE,
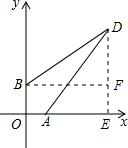
设点D坐标为(x,y),则由图形得:AE2+DE2=AD2,DF2+BF2=BD2,
即
,
解得:
.
即点D的坐标为(
,
).

又∵DB=12,DA=13,
∴DA2=DB2+AB2,
∴△ABD是直角三角形,
故S四边形BOAD=S△AOB+S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点D作DE⊥OA,过点B作BF⊥DE,

设点D坐标为(x,y),则由图形得:AE2+DE2=AD2,DF2+BF2=BD2,
即
|
解得:
|
即点D的坐标为(
| 48 |
| 5 |
| 56 |
| 5 |
点评:此题考查了勾股定理及勾股定理的逆定理,第一问的关键是判断出△ABD是直角三角形,第二问难度较大,注意解方程时要细心.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
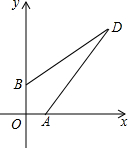 如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13
如图:在以点O为坐标原点的平面直角坐标系中,已知B(0,4),A(3,0),且DB=12,DA=13