题目内容
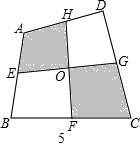
如图1,已知四边形ABCD,点P为平面内一动点.如果∠PAD=∠PBC,那么我们称点P为四边形ABCD关于A、B的等角点.如图2,以点B为坐标原点,BC所在直线为x轴建立平面直角坐标系,点C的横坐标为6.(1)若A、D两点的坐标分别为A(0,4)、D(6,4),当四边形ABCD关于A、B的等角点P在DC边上时,则点P的坐标为
(2)若A、D两点的坐标分别为A(2,4)、D(6,4),当四边形ABCD关于A、B的等角点P在DC边上时,求点P的坐标;
(3)若A、D两点的坐标分别为A(2,4)、D(10,4),点P(x,y)为四边形ABCD关于A、B的等角点,其中x>2,y>0,求y与x之间的关系式.
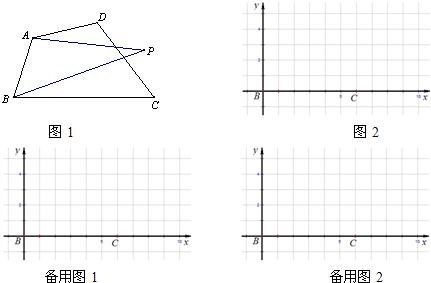
分析:(1)画出点A、D坐标,根据四边形ABCD是矩形可得点P在CD的中点处,写出相应坐标即可;
(2)易得点P的横坐标为6,利用△PAD∽△PBC可得点P的纵坐标;
(3)可分点P在直线AD的上方,或下方两种情况进行探讨:当点P在直线AD的上方时,点P在线段BA的延长线上,利用点A的坐标可得相关代数式;当点P在直线AD的下方时,利用(2)中的相似可得相关代数式.
(2)易得点P的横坐标为6,利用△PAD∽△PBC可得点P的纵坐标;
(3)可分点P在直线AD的上方,或下方两种情况进行探讨:当点P在直线AD的上方时,点P在线段BA的延长线上,利用点A的坐标可得相关代数式;当点P在直线AD的下方时,利用(2)中的相似可得相关代数式.
解答:解:(1)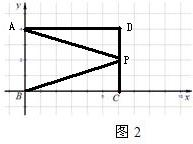
由图中可以看出P(6,2).
故答案为(6,2);
(2)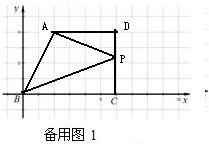
依题意可得∠D=∠BCD=90°,∠PAD=∠PBC,AD=4,CD=4,BC=6.
∴△PAD∽△PBC,
∴
=
=
,
∵PD+PC=CD=4,
∴PC=
.
∴点P的坐标为(6,
);
(3)根据题意可知,不存在点P在直线AD上的情况;
当点P不在直线AD上时,分两种情况讨论:
①当点P在直线AD的上方时,点P在线段BA的延长线上,此时有y=2x;
②当点P在直线AD的下方时,过点P作MN⊥x轴,分别交直线AD、BC于M、N两点,
与(2)同理可得△PAM∽△PBN,PM+PN=4,
由点P的坐标为P(x,y),可知M、N两点的坐标分别为M(x,4)、N(x,0).
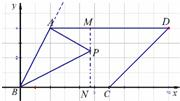
∴
=
.
可得
=
.
∴y=
.
综上所述,当x>2,y>0时,y与x之间的关系式为y=2x或y=
.

由图中可以看出P(6,2).
故答案为(6,2);
(2)

依题意可得∠D=∠BCD=90°,∠PAD=∠PBC,AD=4,CD=4,BC=6.
∴△PAD∽△PBC,
∴
| PD |
| PC |
| AD |
| BC |
| 4 |
| 6 |
∵PD+PC=CD=4,
∴PC=
| 12 |
| 5 |
∴点P的坐标为(6,
| 12 |
| 5 |
(3)根据题意可知,不存在点P在直线AD上的情况;
当点P不在直线AD上时,分两种情况讨论:
①当点P在直线AD的上方时,点P在线段BA的延长线上,此时有y=2x;
②当点P在直线AD的下方时,过点P作MN⊥x轴,分别交直线AD、BC于M、N两点,
与(2)同理可得△PAM∽△PBN,PM+PN=4,
由点P的坐标为P(x,y),可知M、N两点的坐标分别为M(x,4)、N(x,0).

∴
| PM |
| PN |
| AM |
| BN |
可得
| 4-y |
| y |
| x-2 |
| x |
∴y=
| 2x |
| x-1 |
综上所述,当x>2,y>0时,y与x之间的关系式为y=2x或y=
| 2x |
| x-1 |
点评:主要考查了相似三角形的应用;易错点在于分情况探讨等角点的位置;难点在于利用相似三角形的判定与性质得到点P的纵坐标.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目