题目内容
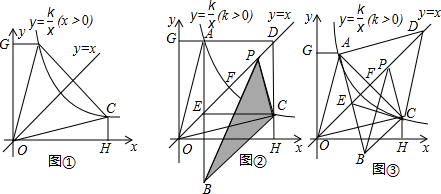
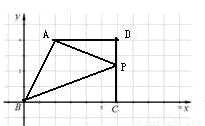
如图1,已知四边形ABCD,点P为平面内一动点.如果∠PAD=∠PBC,那么我们称点P为四边形ABCD关于A、B的等角点. 如图2,以点B为坐标原点,BC所在直线为x轴建立平面直角坐标系,点C的横坐标为6.
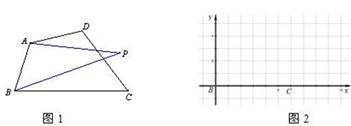
(1)若A、D两点的坐标分别为A(0,4)、D(6,4),当四边形ABCD关于A、B的等角点P在DC边上时,则点P的坐标为 ;
(2)若A、D两点的坐标分别为A(2,4)、D(6,4),当四边形ABCD关于A、B的角点P在DC边上时,求点P的坐标;
(3)若A、D两点的坐标分别为A(2,4)、D(10,4),点P(x,y)为四边形ABCD关于A、B的等角点,其中x>2,y>0,求y与x之间的关系式.
(1)(6,2);(2)(6,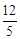 );(3)y=2x或
);(3)y=2x或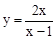 .
.
【解析】
试题分析:(1)画出点A、D坐标,根据四边形ABCD是矩形可得点P在CD的中点处,写出相应坐标即可;(2)易得点P的横坐标为6,利用△PAD∽△PBC可得点P的纵坐标;(3)可分点P在直线AD的上方,或下方两种情况进行探讨:当点P在直线AD的上方时,点P在线段BA的延长线上,利用点A的坐标可得相关代数式;当点P在直线AD的下方时,利用(2)中的相似可得相关代数式.
试题解析:(1)(6,2).
(2)依题意可得∠D=∠BCD=90°,∠PAD=∠PBC,AD=4,CD=4,BC=6.
∴△PAD∽△PBC. ∴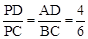 .
.
∵PD+PC=CD=4,∴PC=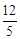 .
.
∴点P的坐标为(6,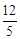 ).
).
(3)根据题意可知,不存在点P在直线AD上的情况;
当点P不在直线AD上时,分两种情况讨论:
①当点P在直线AD的上方时,点P在线段BA的延长线上,此时有y=2x.
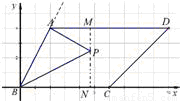
②当点P在直线AD的下方时,过点P作MN⊥x轴,分别交直线AD、BC于M、N两点,
与(2)同理可得△PAM∽△PBN,PM+PN=4,
由点P的坐标为P(x,y),可知M、N两点的坐标分别为M(x,4)、N(x,0).
∴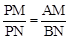 .可得
.可得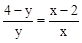 ,即
,即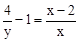 ,即
,即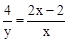 .∴
.∴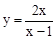 .
.
综上所述,当x>2,y>0时,y与x之间的关系式为y=2x或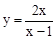 .
.
考点:1.动点问题;2.新定义;3. 坐标与图形的对称变化;4.相似三角形的应用;5.数形结合和分类思想的应用.

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案