Question

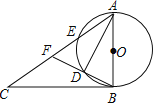
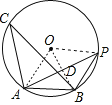
【题目】如图，△ABC是⊙O的内接三角形，∠C＝30°，⊙O的半径是6，若点P是⊙O上的一点，＝，则PA的长为_____．

Answer 1

【答案】6

【解析】

连接OA、OB、OP，根据圆周角定理求得∠APB＝∠C＝30°，进而求得∠PAB＝∠APB＝30°，∠ABP＝120°，根据垂径定理得到OB⊥AP，AD＝PD，∠OBP＝∠OBA＝60°，即可求得△AOB是等边三角形，从而求得PB＝OA＝6，解直角三角形求得PD，即可求得PA．

解：连接OA、OB、OP，

∵∠C＝30°，

∴∠APB＝∠C＝30°，

∵，

∴PB＝AB，

∴∠PAB＝∠APB＝30°

∴∠ABP＝120°，

∵PB＝AB，

∴OB⊥AP，AD＝PD，

∴∠OBP＝∠OBA＝60°，

∵OB＝OA，

∴△AOB是等边三角形，

∴AB＝OA＝6，

则Rt△PBD中，PD＝cos30°PB＝×6＝3，

∴AP＝2PD＝6，

故答案为：6．