题目内容
【题目】如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①![]() ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=![]() AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
AB;④S△ABC=5S△BDF,其中正确的结论序号是( )
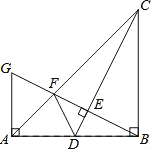
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
【解析】
根据同角的余角相等求出∠ABG=∠BCD,然后利用“角边角”证明△ABG和△BCD
全等,根据全等三角形对应边相等可得AG=BD,然后求出![]() ,再求出△AFG和
,再求出△AFG和
△CFB相似,根据相似三角形对应边成比例可得![]() 从而判断出①正确;求出
从而判断出①正确;求出
![]() ,然后根据FE≠BE判断出②错误;根据相似三角形对应边成比例求出
,然后根据FE≠BE判断出②错误;根据相似三角形对应边成比例求出![]()
再根据等腰直角三角形的性质可得![]() 然后整理即可得到
然后整理即可得到![]() 判断出
判断出
③正确;过点F作MF⊥AB于M,根据三角形的面积整理即可判断出④错误.
∵∠ABC=90°,BG⊥CD,
∴∠ABG+∠CBG=90°,∠BCD+∠CBG=90°,
∴∠ABG=∠BCD,
在△ABC和△BCD中,
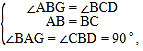
∴△ABG≌和△BCD(ASA),
∴AG=BD,
∵点D是AB的中点,
∴![]()
∴![]()
在Rt△ABC中,∠ABC=90°,
∴AB⊥BC,
∵AG⊥AB,
∴AG∥BC,
∴△AFG∽△CFB,
∴![]()
∵BA=BC,
∴![]() 故①正确;
故①正确;
∵△AFG∽△CFB,
∴![]()
∴![]()
∵FE≠BE,
∴点F是GE的中点不成立,故②错误;
∵△AFG∽△CFB,
∴![]()
∴![]()
∵![]()
∴![]() 故③正确;
故③正确;
过点F作MF⊥AB于M,则FM∥CB,
∴![]()
∵![]()
∴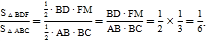 故④错误.
故④错误.
综上所述,正确的结论有①③共2个.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目