题目内容
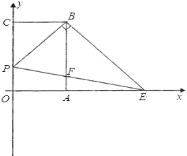
【题目】如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=﹣1,与x轴交于点C,且∠ABC=90°,求:
(1)直线AB的解析式;
(2)抛物线的解析式.

【答案】(1)y=﹣![]() x+2;(2)y=﹣
x+2;(2)y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
【解析】
(1)先证明Rt△CBO∽Rt△BAO,利用相似比计算出OB=2,则B点坐标为(0,2),然后利用待定系数法确定直线AB的解析式;
(2)先利用对称性得到抛物线与x轴的另一个交点坐标为(-6,0),则可设交点式y=a(x+6)(x-4),然后把B点坐标代入求出a即可.
(1)∵A点坐标为(4,0),C点坐标为(﹣1,0),
∴OA=4,OC=1,
∵∠ABC=90°,
∴∠CBO=∠BAO,
∴Rt△CBO∽Rt△BAO,
∴OB:OA=OC:OB,即OB:4=1:OB,
∴OB=2,
∴B点坐标为(0,2),
设直线AB的解析式为y=mx+n,
把A(4,0)、B(0,2)代入得![]() ,解得
,解得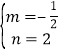 ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
(2)∵该抛物线的对称轴x=﹣1,
而A点坐标为(4,0),
∴抛物线与x轴的另一个交点坐标为(﹣6,0),
设抛物线的解析式为y=a(x+6)(x﹣4),
把B(0,2)代入得a6(﹣4)=2,解得a=﹣![]() ,
,
所以抛物线的解析式为y=﹣![]() (x+6)(x﹣4)=﹣
(x+6)(x﹣4)=﹣![]() x2﹣
x2﹣![]() x+2.
x+2.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目