题目内容
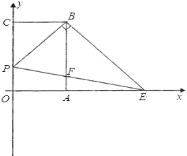
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
【答案】(1)(5,0);(2)存在.
【解析】
(1)本题需先求出AB=AE,再求出DE=5,即可求出点E的坐标.
(2)本题需先求出CP=CB=2,即可求出t的值.(3)本题需先证出△BCP~△BAE,求出
AE= t,再证出△POE~△PCB,求出的t值,再求出OP的长,即可求出P的坐标.
解:(1)当 t=2 时,PC=2,∵BC=2,∴PC=BC,∴∠PBC=45°,∴∠BAE=90°,
∴∠AEB=45°,∴AB=AE=3,OE=5,∴点 E 的坐标是(5,0);
(2)存在,
∵∠ABE+∠ABP=90°
∠PBC+∠ABP=90°
∴∠ABE=∠PBC
∵∠BAE=∠BCP=90°
∴△POE![]() △BAE
△BAE
∴![]() =
=![]()
∴![]() =
=![]()
∴AE=![]() t
t
∵若△POE![]() △PCB
△PCB
∴![]()
∴![]() =
=![]()
![]() ,
,![]() (舍去)
(舍去)
∴P的坐标为(0,![]() ).
).

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目