题目内容
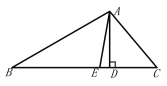
【题目】如图,在Rt△ABC中,∠ACB=90°,D是边BC上一动点(不与B,C重合),DE⊥AB于点E,点F是线段AD的中点,连接EF,CF.
(1)试猜想线段EF与CF的大小关系,并加以证明.
(2)若∠BAC=30°,连接CE,在D点运动过程中,探求CE与AD的数量关系.

【答案】(1)见解析;(2)见解析.
【解析】
(1)EF和CF分别是直角△AED和直角△ACD斜边上的中线,依据直角三角形斜边上的中线等于斜边的一半即可证得;
(2)证明△EFC是等边三角形,然后根据等边三角形的定义以及直角三角形的性质求解.
(1)EF=CF,理由如下:
在Rt△AED和Rt△ACD中,
∵点F是线段AD的中点,
∴EF=![]() AD,CF=
AD,CF=![]() AD,
AD,
∴EF=CF;
(2)由(1)可知,EF=AF=CF,
∴∠AEF=∠EAF,∠ACF=∠CAF,
∴∠EFD=2∠EAF,∠CFD=2∠CAF,
∴∠EFC=2∠BAC=60°,
又EF=CF,
∴△EFC为等边三角形,
∴CE=EF=![]() AD.
AD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目