题目内容
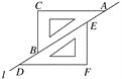
【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.

【答案】(1)见解析;(2)见解析.
【解析】
(1)因为AF∥DC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,得出AF=DC即可;
(2)由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又由AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
(1)∵AF∥DC,
∴∠AFE=∠DCE,
又∵E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,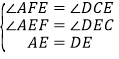 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC;
(2)当AD=CF时,四边形AFDC是矩形;理由如下:
由(1)得:AF=DC且AF∥DC,
∴四边形AFDC是平行四边形,
又∵AD=CF,
∴四边形AFDC是矩形(对角线相等的平行四边形是矩形).

练习册系列答案
相关题目