题目内容
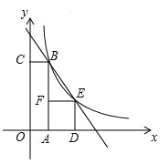
【题目】如图,矩形ABCD中,AB=5,BC=8,点E为AD上一个动点,把△ABE沿BE折叠,点A的对应点为点F,连接DF,连接CF.当点F落在矩形内部,且CF=CD时,AE的长为( ).
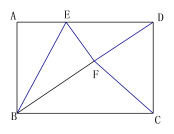
A. 3B. 2.5C. 2D. 1.5
【答案】B
【解析】
过点F作FM⊥BC于点M,延长MF交AD于点N,可得四边形ABMN是矩形,
.因为AB=CD=BF=CF=5,所以△BFC是等腰三角形,由三线合一可得BM=5,由勾股定理可得MF=3,从而求得FN=2,设AE=x,则AE=x=EF,EN=AN-AE=4-x,在Rt△EFN中,因为EF2=EN2+NF2,所以x2=(4-x)2+22,从而解得:x=2.5.
解:过点F作FM⊥BC于点M,延长MF交AD于点N,由折叠知Rt△ABE≌△FBE,AB=FB=5,AE=FE,
又∵CF=CD=5
∴BM=CM=4,
Rt△BMF中,MF=![]() =
=![]() =3,
=3,
∵∠A=∠B=∠BMN=90°
∴四边形ABMN是矩形,MN=AB=5,AN=BM=4,NF=MN-MF=5-3=2,
设AE=x,则AE=x=EF,EN=AN-AE=4-x,
Rt△EFN中,∵EF2=EN2+NF2
∴x2=(4-x)2+22,解得:x=2.5

故选:B.

练习册系列答案
相关题目