题目内容
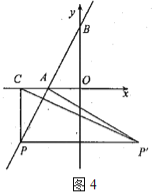
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(﹣4,0),点B的坐标是(0,b)(b>0).P是直线AB上的一个动点,作PC⊥x轴,垂足为C.记点P关于y轴的对称点为P(点P不在y轴上),连接PP,PA,PC.设点P的横坐标为a.
(1)当b=3时,
①求直线AB的解析式;
②若点P′的坐标是(﹣1,m),求m的值;
(2)若点P在第一象限,记直线AB与PC的交点为D.当PD:DC=1:3时,求a的值;
(3)是否同时存在a,b,使△PCA为等腰直角三角形?若存在,请求出所有满足要求的a,b的值;若不存在,请说明理由.
【答案】解:(1)①设直线AB的解析式为y=kx+3,
把x=﹣4,y=0代入得:﹣4k+3=0,
∴k=![]() ,
,
∴直线的解析式是:y=![]() x+3,
x+3,
②由已知得点P的坐标是(1,m),
∴m=![]() ×1+3=
×1+3=![]() ;
;
(2)∵PP′∥AC,
△PP′D∽△ACD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴a=![]() ;
;
(3)以下分三种情况讨论.
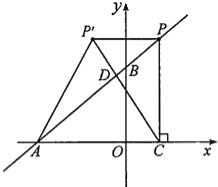
①当点P在第一象限时,
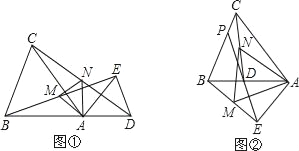
1)若∠AP′C=90°,P′A=P′C(如图1)
过点P′作P′H⊥x轴于点H.
∴PP′=CH=AH=P′H=![]() AC.
AC.
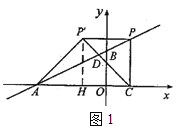
∴2a=![]() (a+4)
(a+4)
∴a=![]()
∵P′H=PC=![]() AC,△ACP∽△AOB
AC,△ACP∽△AOB
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴b=2
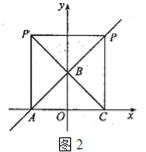
2)若∠P′AC=90°,P′A=CA
则PP′=AC
∴2a=a+4
∴a=4
∵P′A=PC=AC,△ACP∽△AOB
∴![]() =
=![]() =1,即
=1,即![]() =1
=1
∴b=4
3)若∠P′CA=90°,
则点P′,P都在第一象限内,这与条件矛盾.
∴△P′CA不可能是以C为直角顶点的等腰直角三角形.
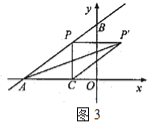
②当点P在第二象限时,∠P′CA为钝角(如图3),此时△P′CA不可能是等腰直角三角形;
③当P在第三象限时,∠P′CA为钝角(如图4),此时△P′CA不可能是等腰直角三角形.
∴所有满足条件的a,b的值为
![]() 或
或![]()
【解析】略

 口算题天天练系列答案
口算题天天练系列答案【题目】已知y是x的函数,自变量x的取值范围是x≠0的全体实数,如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … |
|
| ﹣ | ﹣ | ﹣ |
|
|
| m |
| … |
小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)从表格中读出,当自变量是﹣2时,函数值是 ;
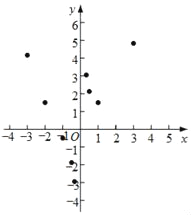
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(3)在画出的函数图象上标出x=2时所对应的点,并写出m= .
(4)结合函数的图象,写出该函数的一条性质: .