题目内容
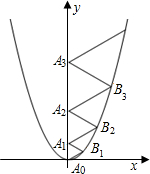 二次函数y=
二次函数y=| 2 | 3 |
分析:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,设A0A1=a,A1A2=b,A2A3=c,则AB1=
a,BB2=
b,CB3=
c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y=
x2中,求a、b、c的值,得出规律.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 3 |
解答: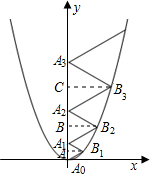 解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
设A0A1=a,A1A2=b,A2A3=c,则AB1=
a,BB2=
b,CB3=
c,
在正△A0B1A1中,B1(
a,
),
代入y=
x2中,得
=
•(
a)2,解得a=1,即A0A1=1,
在正△A1B2A2中,B2(
b,1+
),
代入y=
x2中,得1+
=
•(
b)2,解得b=2,即A1A2=2,
在正△A2B3A3中,B3(
c,3+
),
代入y=
x2中,得3+
=
•(
c)2,解得c=3,即A2A3=3,
由此可得△A2009B2010A2010的边长=2010.
故答案为:2010.
 解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,设A0A1=a,A1A2=b,A2A3=c,则AB1=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
在正△A0B1A1中,B1(
| ||
| 2 |
| a |
| 2 |
代入y=
| 2 |
| 3 |
| a |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
在正△A1B2A2中,B2(
| ||
| 2 |
| b |
| 2 |
代入y=
| 2 |
| 3 |
| b |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
在正△A2B3A3中,B3(
| ||
| 2 |
| c |
| 2 |
代入y=
| 2 |
| 3 |
| c |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
由此可得△A2009B2010A2010的边长=2010.
故答案为:2010.
点评:本题考查了二次函数的综合运用.关键是根据正三角形的性质表示点的坐标,利用抛物线解析式求正三角形的边长,得到规律.

练习册系列答案
相关题目
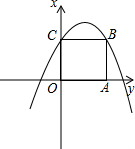 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-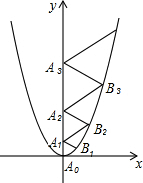 二次函数
二次函数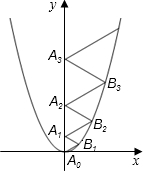 二次函数
二次函数