题目内容
 二次函数y=
二次函数y=| 2 |
| 3 |
| 2 |
| 3 |
1
1
,△A2010B2011A2011的边长=2011
2011
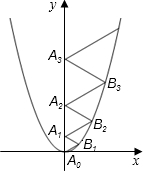
.分析:先计算出△A0B1A1;△A1B2A2;△A2B3A2的边长,推理出各边长组成的数列各项之间的排列规律,依据规律得到△A2010B2011A2011的边长.
解答: 解:作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.
解:作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.
设等边△A0B1A1、△A1B2A2、△A2B3A3中,AA1=a,BA2=b,CA2=c.
①等边△A0B1A1中,A0A=a,
所以B1A=atan60°=
a,代入解析式得
×(
a)2=a,解得a=0(舍去)或a=
,于是等边△A0B1A1的边长为
×2=1;
②等边△A1B2A2中,A1B=b,
所以BB2=btan60°=
b,B2点坐标为(
b,1+b)代入解析式得
×(
b)2=1+b,
解得b=-
(舍去)或b=1,
于是等边△A1B2A2的边长为1×2=2;
③等边△A2B3A3中,A2C=c,
所以CB3=btan60°=
c,B3点坐标为(3c,3+c)代入解析式得
×(
c)2=3+c,
解得c=-1(舍去)或c=
,
于是等边△A2B3A3的边长为
×2=3.
于是△A2010B2011A2011的边长为2011.
 解:作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.
解:作B1A⊥y轴于A,B2B⊥y轴于B,B3C⊥y轴于C.设等边△A0B1A1、△A1B2A2、△A2B3A3中,AA1=a,BA2=b,CA2=c.
①等边△A0B1A1中,A0A=a,
所以B1A=atan60°=
| 3 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
②等边△A1B2A2中,A1B=b,
所以BB2=btan60°=
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
解得b=-
| 1 |
| 2 |
于是等边△A1B2A2的边长为1×2=2;
③等边△A2B3A3中,A2C=c,
所以CB3=btan60°=
| 3 |
| 2 |
| 3 |
| 3 |
解得c=-1(舍去)或c=
| 3 |
| 2 |
于是等边△A2B3A3的边长为
| 3 |
| 2 |
于是△A2010B2011A2011的边长为2011.
点评:本题考查的是二次函数综合题,此题将二次函数和等边三角形的性质结合在一起,是一道开放题,有利于培养同学们的探索发现意识.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
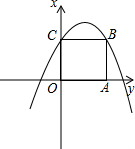 如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-
如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数y=-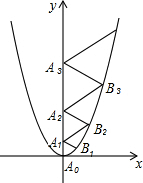 二次函数
二次函数