题目内容
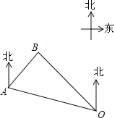
【题目】如图,一艘巡逻船在海上![]() 处巡航,突然接到海上指挥中心
处巡航,突然接到海上指挥中心![]() 处发出的紧急通知,在巡逻船的东北方向的
处发出的紧急通知,在巡逻船的东北方向的![]() 处有一艘渔船遇险,要马上前去救援,已知点
处有一艘渔船遇险,要马上前去救援,已知点![]() 位于指挥中心
位于指挥中心![]() 的北偏西
的北偏西![]() 方向上,且相距
方向上,且相距![]() 海里,渔船位于指挥中心
海里,渔船位于指挥中心![]() 的北偏西
的北偏西![]() 方向上,求
方向上,求![]() 、
、![]() 两地之间的距离.(结果精确到
两地之间的距离.(结果精确到![]() 海里,参考数据:
海里,参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】![]() 、
、![]() 两地之间的距离约为
两地之间的距离约为![]() 海里
海里
【解析】
作BC⊥OA于点C,根据题意得∠MAB=45°,∠NOA=60°,∠NOB=30°,OA=60海里.由AM∥ON,求出∠BAO=∠MAO-∠MAB=75°,根据三角形内角和定理得出∠ABO=180°-∠BAO-∠AOB=75°,利用等角对等边得到OB=OA=60海里,在直角△OBC中根据含30°角的直角三角形的性质得出BC=![]() OB=30海里,OC=
OB=30海里,OC=![]() BC=30
BC=30![]() 海里,那么AC=OA-OC=(60-30
海里,那么AC=OA-OC=(60-30![]() )≈8.04海里,然后根据勾股定理求出AB=
)≈8.04海里,然后根据勾股定理求出AB=![]() ≈31.1海里.
≈31.1海里.
如图,作BC⊥OA于点C,
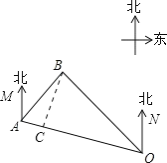
根据题意得∠MAB=45,∠NOA=60,∠NOB=30,OA=60海里,
∵AM∥ON,
∴∠MAO+∠NOA=180,
∴∠MAO=180∠NOA=120,
∴∠BAO=∠MAO∠MAB=75,
∵∠AOB=∠NOA∠NOB=30,
∴∠ABO=180∠BAO∠AOB=75,
∴∠BAO=∠ABO=75,
∴OB=OA=60海里,
∴BC=![]() OB=30海里,OC=
OB=30海里,OC=![]() BC=30
BC=30![]() 海里,
海里,
∴AC=OAOC=(6030![]() )≈8.04海里,
)≈8.04海里,
∴AB=![]() ≈
≈![]() ≈31.1海里.
≈31.1海里.
答:A、B两地之间的距离约为31.1海里.

练习册系列答案
相关题目