题目内容
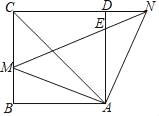
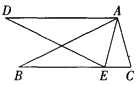
【题目】如图，在矩形ABCD中，AB＝6，BC＝10，将矩形ABCD沿BE折叠，点A落在A'处，若EA'的延长线恰好过点C，则sin∠ABE的值为_____．
【答案】
【解析】
根据勾股定理求出A'C，在利用勾股定理建立方程求出AE，即可求出BE，最后利用三角关系得出结论.
解：由折叠知，A'E＝AE，A'B＝AB＝6，∠BA'E＝90°，
∴∠BA'C＝90°，
在Rt△A'CB中，A'C＝
＝8，
设AE＝x，则A'E＝x，
∴DE＝10﹣x，CE＝A'C+A'E＝8+x，
在Rt△CDE中，根据勾股定理得，（10﹣x）2+36＝（8+x）2，
∴x＝2，
∴AE＝2，
在Rt△ABE中，根据勾股定理得，BE＝
＝2
，
∴sin∠ABE＝
＝，
故答案为：．
练习册系列答案
相关题目
