题目内容
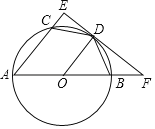
【题目】如图,已知AB为⊙O的直径,AC是⊙O的弦,D是弧BC的中点,过点D作⊙O的切线,分别交AC、AB的延长线于点E和点F,连接CD、BD.
(1)求证:∠A=2∠BDF;
(2)若AC=3,AB=5,求CE的长.
【答案】(1)见解析;(2)1
【解析】
(1)连接AD,如图,利用圆周角定理得∠ADB=90°,利用切线的性质得OD⊥DF,则根据等角的余角相等得到∠BDF=∠ODA,所以∠OAD=∠BDF,然后证明∠COD=∠OAD得到∠CAB=2∠BDF;
(2)连接BC交OD于H,如图,利用垂径定理得到OD⊥BC,则CH=BH,于是可判断OH为△ABC的中位线,所以OH=1.5,则HD=1,然后证明四边形DHCE为矩形得到CE=DH=1.
(1)证明:连接AD,如图,

∵AB为⊙O的直径,
∴∠ADB=90°,
∵EF为切线,
∴OD⊥DF,
∵∠BDF+∠ODB=90°,∠ODA+∠ODB=90°,
∴∠BDF=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠BDF,
∵D是弧BC的中点,
∴∠COD=∠OAD,
∴∠CAB=2∠BDF;
(2)解:连接BC交OD于H,如图,
∵D是弧BC的中点,
∴OD⊥BC,
∴CH=BH,
∴OH为△ABC的中位线,
∴![]() ,
,
∴HD=2.5-1.5=1,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴四边形DHCE为矩形,
∴CE=DH=1.

 ABC考王全优卷系列答案
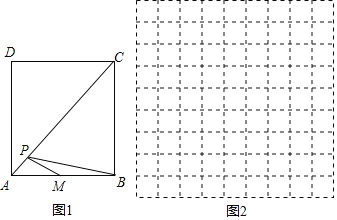
ABC考王全优卷系列答案【题目】在正方形ABCD中,AB=4cm,AC为对角线,AC上有一动点P,M是AB边的中点,连接PM、PB,设A、P两点间的距离为xcm,PM+PB长度为ycm.
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y/cm | 6.0 | 4.8 | 4.5 | 6.0 | 7.4 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:PM+PB的长度最小值约为______cm.
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.
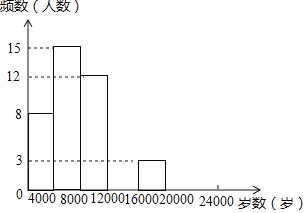
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.