题目内容
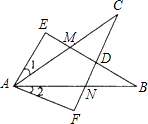
如图△ABC中,过点A分别作∠ABC、∠ACB的外角的平分线的垂线AD,AE,D,E为垂足.
求证:(1)ED∥BC;
(2)ED=
(AB+AC+BC).

求证:(1)ED∥BC;
(2)ED=
| 1 |
| 2 |

证明:(1)分别延长AD、AE与直线BC交于点F、G,
∵AD⊥BD,
∴∠ADB=∠FDB=90°,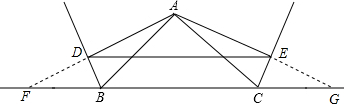
∵BD=BD,∠ABD=∠FBD,
∴△ABD≌△FBD
∴AD=FD,
同理可得AE=EG,
∴DE∥BC;
(2)由(1)知△ABD≌△FBD,
∴AB=BF,
同理AC=CG,
∵DE=
FG
∴GF=FB+BC+GC=AB+BC+AC,
∴DE=
(AB+BC+AC).
∵AD⊥BD,
∴∠ADB=∠FDB=90°,

∵BD=BD,∠ABD=∠FBD,
∴△ABD≌△FBD
∴AD=FD,
同理可得AE=EG,
∴DE∥BC;
(2)由(1)知△ABD≌△FBD,
∴AB=BF,
同理AC=CG,
∵DE=
| 1 |
| 2 |
∴GF=FB+BC+GC=AB+BC+AC,
∴DE=
| 1 |
| 2 |

练习册系列答案
相关题目