题目内容
【题目】如图,在△ABC中,∠ABC,∠ACB的平分线的交点P恰好在BC边的高AD上,则△ABC一定是( )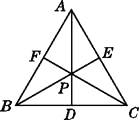
A.直角三角形
B.等边三角形
C.等腰三角形
D.等腰直角三角形
【答案】C
【解析】解:∵∠ABC与∠ACB的平分线的交点P,
∴点P是△ABC的内心,
∴AD是顶角的平分线,
∴∠BAD=∠CAD ,
又∵AD是BC上的高,
∴∠ADB=∠ADC ,
又∵AD=AD
∴△ADB≌△ADC,
∴AB=AC.
∴△ABC一定是等腰三角形.
故应选:C.
根据角平分线的性质得出点P是△ABC的内心,进而得出AD是顶角的平分线,根据角平分线的定义得出∠BAD=∠CAD ,根据垂直的定义得出∠ADB=∠ADC ,然后利用ASA判断出△ADB≌△ADC,根据全等三角形对应边相等得出AB=AC,从而得出结论。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目